Расчета уклона формула: Калькулятор уклонов
Как рассчитать угол наклона крыши с примерами
Крыши зданий и сооружений делятся на две категории: плоские и наклонные. В этой статье будет разбираться со второй позицией, а точнее, с углом наклона крыши: какие характеристики влияют на данный параметр, какие кровельные материалы под каким углом кровли укладываются, в каких единицах изменяется угол наклона скатов. Разобравшись в полученной информации, Вы легко сможете контролировать правильность сооружения крыши вашего дома.
Угол наклона крышиИсточник goldkryshi.ru
Единицы измерения угла ската
Из школьного курса геометрии все знают, что величина любого угла измеряется в градусах. Уклон кровли в этом случае – не исключение. Но необходимо обозначить, что в технической литературе, в ГОСТах и справочниках встречают и другие единицы измерения. А именно: проценты и отношения сторон.
В первую очередь надо обозначить, что подразумевают под углом ската крыши. На фото ниже он обозначен латинской буквой альфа.
На фото ниже он обозначен латинской буквой альфа.
Угол наклона ската кровлиИсточник remontik.org
В строительной сфере крыши с углом наклона выше 50° встречаются редко. К ним можно отнести башенки в готическом стиле или нижние скаты мансардных кровель. В основном максимальный параметр – 45°.
Что касается двух других единиц измерения, то отношение сторон – это так называемая упрощенная дробь. В ее основе лежат два размера: высота крыши, на фото она обозначена буквой «Н», и проекцией ската, обозначенная буквой «L». Соотношение должно быть таким: Н/L.
Добавим, что проекция длины ската – это, по сути, половина ширины дома, если крыша двускатная симметричная, или полная ширина, если крыша односкатная. При этом угол наклона так и пишется дробью, к примеру, 1:3.
В некоторых конструкций обозначение дробью неудобно. К примеру, если она выглядит вот так: 4:13. Поэтому используют процентное исчисление. Оно рассчитывается таким образом:
4:13х100=30,77%
Уклон кровли в процентах и градусах используется профессиональными строителями чаще, чем отношение сторон, потому что такое обозначение применяется в справочниках и технической литературе. То есть это чисто технические единицы измерения. Хотя перевести из одной единицы измерения в другую не сложно. На фото ниже показан перевод из градусов и отношении я сторон и наоборот.
То есть это чисто технические единицы измерения. Хотя перевести из одной единицы измерения в другую не сложно. На фото ниже показан перевод из градусов и отношении я сторон и наоборот.
Пропорции соотношения градусов к размерам крышиИсточник obustroeno.com
Если есть необходимость перевести градусы в проценты, то, исходя из рисунка выше, можно сделать несколько математических выкладок. За 100% берется угол, равный 45°. Теперь можно найти, сколько градусов в одном проценте. Для этого надо:
45/100=0,45°. Переводим в минуты, получается 27’. То есть 1% – это 27 градусных минут.
Можно подойти к решению поставленной задачи с обратной стороны. То есть перевести градусы в проценты. Здесь обратное соотношение:
100/45=2,22%
Получается так, что в одном градусе 2,22%.
Зависимость угла наклона ската и типа кровельного материала
Вышу уже говорилось о двух разновидностях кровель: плоские и наклонные. Но надо отметить, что у плоских кровель тоже есть свой угол, который варьируется в диапазоне 0-5°. Скатные крыши делятся на две подгруппы (деление условное):
Но надо отметить, что у плоских кровель тоже есть свой угол, который варьируется в диапазоне 0-5°. Скатные крыши делятся на две подгруппы (деление условное):
- с небольшим уклоном – от 6 до 30°;
- с крутым уклоном – больше 30°.
Распределение кровельных материалов по крутизне скатаИсточник belhouse.by
У каждого вида кровельных конструкций есть свои преимущества и недостатки. К примеру, плоские – это небольшая площадь покрытия, что позволяет сэкономить на кровельном материале (его количестве). Но при этом такая конструкция потребует проведения усиленной гидроизоляции. Крутые скаты – это беспроблемное схождение атмосферных осадков, но высокая парусность конструкции, что потребует от ее сооружения усиления стропильной системы.
Учитывая это, необходимо строго подходить к выбору кровельного материала. Их производители обязательно информируют потребителей, при каком минимальном уклоне кровли их можно использовать. На фото ниже показана диаграмма распределения кровельных материалов по углам скатов.
На фото ниже показана диаграмма распределения кровельных материалов по углам скатов.
Как видно из диаграммы, на плоских крышах обычно используют рулонные материалы в виде рубероида или толи. Хотя нет никаких противопоказания применения листовых или плитных изделий: шифер, профнастил, листовое железо, собираемое фальцовым способом. А вот штучный кровельный материал лучше на крышах крутизною меньше 15° не использовать. Есть высокая вероятность проникновения воды через стыки элементов покрытия.
Значение угла кровли в градусах и процентах по отношению к типу кровельного материалаИсточник remotvet.ru
Конструктивные особенности крыши в зависимости от угла наклона
Если в проекте дан уклон крыши, то рассчитать ее высоту не составит труда. А этот параметр – один из самых важных, потому что он определяет высоту конька. Этот элемент кровельной конструкции – точка отправления в сооружении крыши в целом.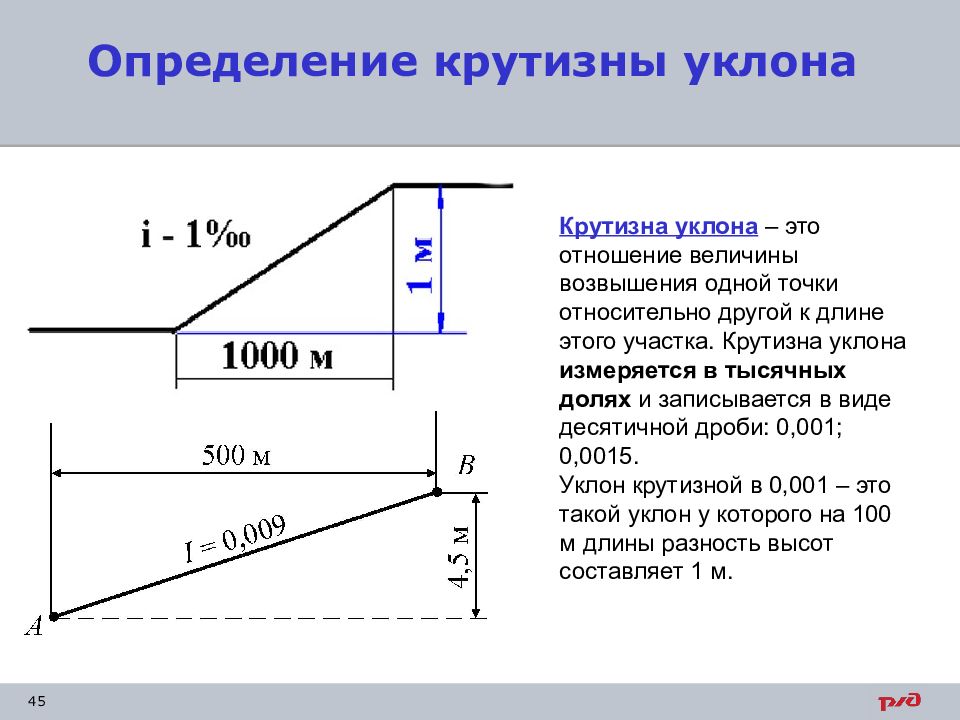 Потому что при строительстве сначала выставляют уровень расположения конька, и уже под него режут пиломатериал: опорные стойки. Отсюда же рассчитывают длину стропильных ног.
Потому что при строительстве сначала выставляют уровень расположения конька, и уже под него режут пиломатериал: опорные стойки. Отсюда же рассчитывают длину стропильных ног.
Сложность расчета заключается в том, что не все помнят тригонометрию, формулы которой используются для расчетов длин элементов кровельного сооружения. В основе формул лежат тригонометрические функции: синус, косинус, тангенс, катангенс.
К примеру, как определить высоту конька (соответственно и крыши) через синус и тангенс:
sin α = H/S, где «S» – это длина ската. Соответственно высота конька будет равна: Н=S x sin α.
tg α = H / L , то есть Н= l x tg α
Точно также можно определить длину ската, или, зная оба параметра, можно рассчитать угол наклона крыши. Все параметры конструкции взаимосвязаны, так что, зная два из них, можно определить третий.
Вентиляция подкровельного пространства: когда нужна и какие применяются методы
Кстати, определяя параметры крыши, можно обойтись и без угла наклона. Для этого используется формула Пифагора. Вот ее формула:
Для этого используется формула Пифагора. Вот ее формула:
S2= H2+ L2
Меняя местами значения, находится необходимая величина.
У Вас может возникнуть вопрос, связанный со значением величин тригонометрических функций. Они в свободном доступе есть, но чтобы Вы их не искали на просторах интернета и не тратили свое время, предлагаем таблицу:
Значения тригонометрических функций от величины углаИсточник remont-kvartiri.livejournal.com
Добавим, что тригонометрические функции упрощают проведения расчетов кровельных конструкций. Если правильно ими пользоваться и уметь набрасывать на бумаге эскизы крыш (имея воображение в плане конструктивного расположения ее элементов), то можно легко рассчитать размеры каждого элемента.
Это касается не только одно- или двускатных сооружений. Также легко можно будет рассчитать и элементы вальмовых или мансардных крыш. Просто придется разбить их сложные конструкции на простые.
Также легко можно будет рассчитать и элементы вальмовых или мансардных крыш. Просто придется разбить их сложные конструкции на простые.
Влияние угла наклона на объем помещения мансарды
Если дом возводится с мансардой, то угол наклона скатов приобретает прикладное значение. И здесь соотношение прямое, то есть чем больше угол, тем больше объем мансарды. Чтобы было понятно, на фото ниже это хорошо видно.
Соотношение угла наклона скатов к объему мансардного помещенияИсточник legkovmeste.ru
Приведем пример, основанный на верхнем рисунке. Здесь четко видно, что высота помещения зависит от параметров наклона крыши. При этом надо учитывать, что оптимальная высота не должна быть меньше 2,5 м. А значит, угол наклона скатов мансарды минимально должна быть 25°. Но обратите внимание, что при таком расположении элементов кровли не учтен объем помещения. То есть ширина комнаты не будет больше 3 м. Это притом, что ширина дома – 10 м. Получается, что используется всего лишь 30% от пространства.
Получается, что используется всего лишь 30% от пространства.
А значит, надо увеличивать значение угла. И чем больше он, тем больше полезная площадь мансарды. Но здесь есть обратная сторона медали. Увеличивая угол, увеличивается высота конька. А это расходы стройматериалов на возведение крыши, плюс увеличение парусности конструкции. Поэтому очень важно найти золотую середину. К примеру, 40° практически решают все проблемы.
Чтобы отойти от этих проблем раз и навсегда, строители давно применяют совершенно другую конструкцию. Она сложна и в сооружении, и в проведении расчетов, но этот вариант решает проблему полезной площади помещения, не увеличивая высоту крыши.
Конструкция мансардной крышиИсточник ok.ru
Расчет высоты конька и угла наклона крыши:
Онлайн калькулятор расчета кровли: тонкости расчета и проверка результатов
Заключение по теме
Проведение расчетов кровельной конструкции – прерогатива специалистов. Потому что правильный расчет, того же угла наклона, это надежность крыши в целом. Но ориентироваться в некоторых технических понятиях будет полезно и владельцам строящихся домов.
Потому что правильный расчет, того же угла наклона, это надежность крыши в целом. Но ориентироваться в некоторых технических понятиях будет полезно и владельцам строящихся домов.
объясняем подробно и с наглядными примерами
При проектировании дома расчет угла наклона крыши — обязательный этап, поскольку от уклона ската зависят нагрузки на кровлю. И не только они. Но иногда нужно рассчитать уклон крыши и для уже построенного дома — например, если планируется реконструкция кровли, а проектная документация утеряна.
В этой статье мы расскажем и о том, как рассчитать наклон крыши существующего дома, и о вычислении и подборе оптимального уклона кровли для строящегося здания. Максимально подробно и с наглядными примерами.
Обычно угол наклона скатов считают по факту. По двум причинам.
Во-первых, никто не даст гарантии, что строители точно выдержали все размеры. И в некоторых случаях разница может быть значительной.
Во-вторых, если дом деревянный, то он неизбежно усаживается в течение первых лет после постройки. И во время этой усадки угол наклона крыши тоже меняется, причем это изменение не поддается расчетам: усадка может быть и 1%, и 3%, и даже 5% и более.
И во время этой усадки угол наклона крыши тоже меняется, причем это изменение не поддается расчетам: усадка может быть и 1%, и 3%, и даже 5% и более.
Пример, как может измениться угол наклона крыши при усадке деревянного дома
Поэтому, если вам нужно знать уклон кровли, лучше не ориентируйтесь на документацию.
Зачем вообще нужно знать угол кровли
Угол наклона крыши нужен для расчета полной нагрузки на скаты кровли. Кроме того, от уклона зависит частота обрешетки, величина нахлестов, подход к устройству примыканий и ряд других тонкостей, вплоть до невозможности использования некоторых видов материалов на слишком крутых или, наоборот, чрезмерно пологих скатах.
Это значит, что расчет угла наклона кровли существующего дома необходим, если ваша цель:
- Перекрытие кровли более тяжелым кровельным материалом. Разница в весе между разными видами кровельных покрытий достигает 45 кг/м2, и это существенная дополнительная нагрузка на стропильную систему.

- Утепление холодной кровли. Это тоже дополнительный вес, хотя обычно играет роль не сам утеплитель, а обрешетка для него.
- Укрепление стропильной системы. Если такая необходимость в принципе возникла, значит, стропильная система уже не держит нагрузку. Следовательно, нужно заново сделать полный расчет стропильной системы, чтобы понять, что именно и как требуется исправить.
- Установка на кровлю солнечных батарей. В зависимости от типа и исполнения солнечные панели весят от 10 до 15 кг на 1 м2. Не каждая кровля выдержит такое увеличение статической нагрузки.
Проще говоря, для ремонта кровли почти всегда нужно знать угол ее наклона. Особенно если ремонт капитальный.
Еще угол наклона нужно рассчитывать, чтобы проверить работу строителей. Конечно, если вы не хотите пополнить армию владельцев домов, у которых в проекте одни цифры, а в реальности — совсем другие.
Как узнать угол наклона крыши существующего дома
Размеры существующих конструкций можно узнать двумя способами: измерить их или рассчитать, если нужного для измерения инструмента нет.
Инструментальные способы
Для измерения угла наклона кровли используют два вида инструментов:
- угломеры;
- уклономеры.
Угломеры — это инструменты, состоящие из двух планок, которые подвижно соединены с одной из сторон. Чтобы измерить уклон ската кровли, одну из планок прижимают к нижней поверхности стропил, а вторую — к коньку, на которую стропильная нога опирается, или к стойке. Это повторяют 7-8 раз с разными стропилами, так как рассчитать угол крыши по одному измерению не получится: ширина некалиброванных досок — а именно их чаще всего используют в качестве стропил — может спокойно отличаться на 10-15 мм. И это не между разными досками, а по длине одной.
Чтобы высчитать угол наклона крыши как можно точнее, измерения, которые дали самые большие и самые маленькие углы, не учитывают, а по остальным вычисляется среднее значение. Например, вы провели восемь замеров уклона ската и получили такие значения:
| Номер замера | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Значение угла | 29,9° | 30,5° | 28,3° | 30,1° | 29,7° | 30,0° | 29,9° | 28,8° |
Результаты измерений №№2, 3 и 8 сильно выбиваются из ряда.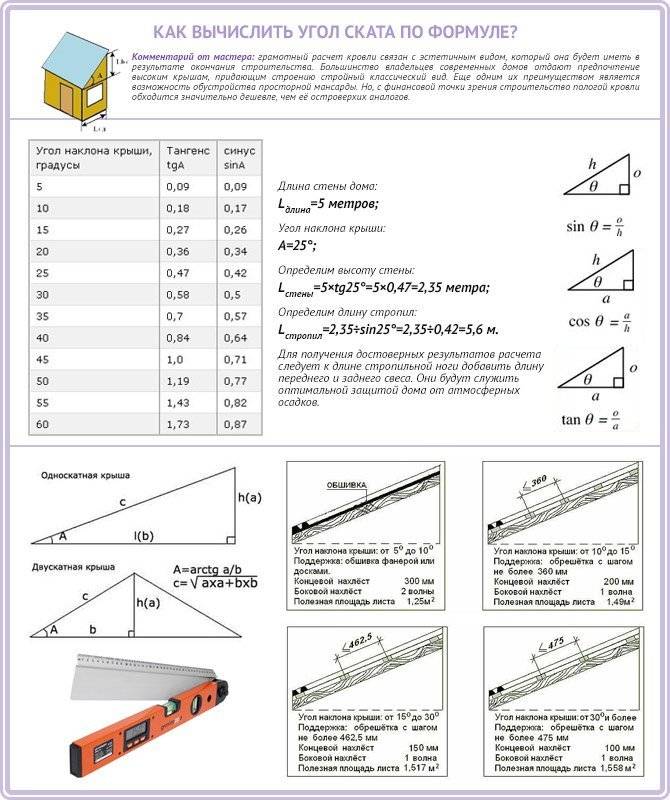 Это значит, что либо стропила установлены неправильно и не выведены в плоскость, либо были какие-то отклонения во время измерений. Если вы только принимаете работы по монтажу стропильной системы, то первый вариант стоит проверить. Если же речь о готовой крыше, то эти измерения просто отбрасываются, а расчёт угла наклона крыши выполняется по оставшимся пяти замерам. В результате средний угол получается равным 29,92°.
Это значит, что либо стропила установлены неправильно и не выведены в плоскость, либо были какие-то отклонения во время измерений. Если вы только принимаете работы по монтажу стропильной системы, то первый вариант стоит проверить. Если же речь о готовой крыше, то эти измерения просто отбрасываются, а расчёт угла наклона крыши выполняется по оставшимся пяти замерам. В результате средний угол получается равным 29,92°.
Подход с отбрасыванием крайних значений и усреднением результата используется при любых измерениях. Независимо от используемого инструмента.
Угломеры бывают механическими и электронными. Хотя чистая механика встречается все реже — угол в ней определяется с помощью шкалы, поэтому для работы с таким угломером нужно хорошее освещение. А под кровлей со светом могут быть проблемы. В электронных угломерах установлен датчик, который определяет, насколько планки смещены друг относительно друга, при этом значение угла сразу же отображается на дисплее.
В отличие от угломеров, уклономеры бывают только электронными. В их основе лежат датчики-инклинометры, которые измеряют уклон относительно гравитационного поля Земли. Следовательно, уклономеры намного точнее, и пользоваться ими проще: нужно просто поставить прибор на стропило, чтобы получить угол его наклона. Если стропильная система уже закрыта кровельным покрытием, уклономер можно прижать к нижней части стропильной ноги, но точность измерений в этом случае будет ниже.
В их основе лежат датчики-инклинометры, которые измеряют уклон относительно гравитационного поля Земли. Следовательно, уклономеры намного точнее, и пользоваться ими проще: нужно просто поставить прибор на стропило, чтобы получить угол его наклона. Если стропильная система уже закрыта кровельным покрытием, уклономер можно прижать к нижней части стропильной ноги, но точность измерений в этом случае будет ниже.
Расчетные методы
Если у вас есть угломер или уклономер, то проблем с измерением уклона скатов не будет. Но как вычислить угол наклона крыши, если этих инструментов под рукой нет? В этом случае на помощь приходит геометрия.
Кровлю любой сложности можно легко представить в виде комбинации прямоугольных треугольников, где:
- скат кровли — это гипотенуза треугольника;
- высота кровли — один из катетов;
- горизонтальное расстояние между коньком кровли и крайней точкой карниза ската — второй катет.
Следовательно, чтобы рассчитать наклон крыши, нужно обычной рулеткой измерить высоту кровли h до верхней точки конька и расстояние от конька до карнизного свеса l.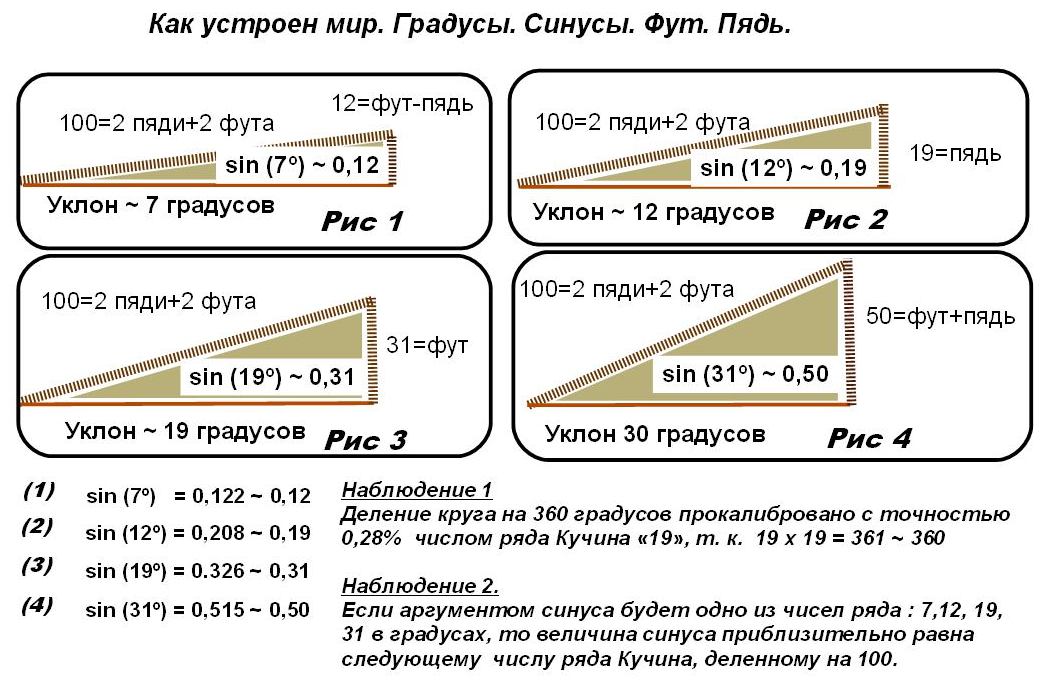 Дальше уклон ската α считается по простой формуле:
Дальше уклон ската α считается по простой формуле:
α = (h/l)·100%
Так вы получите угол наклона ската в процентах. Например, если высота кровли 4 м, а расстояние между ним и карнизом — 10 м, то уклон будет равен 40%.
Знать уклон в процентах не всегда достаточно — во многих строительных стандартах значения указаны в градусах. Поэтому при расчете нужно сделать еще один шаг — перевести полученное значение в градусы. И вот для этой цели простой формулы нет: зависимость нелинейная. Зато есть простая схема:
На схеме показано, как узнать угол наклона крыши в градусах, если есть его величина в процентах. Для этого найдите нужное значение в процентах на вертикальной шкале и посмотрите, какому углу на транспортире оно соответствует.
С готовым домом разобрались. Теперь расскажем о том, как посчитать уклон кровли в градусах, если вы занимаетесь проектированием крыши. Точнее, даже не рассчитать, а подобрать, но об этом чуть позже.
Расчет постоянной нагрузки на скаты кровли
Итак, чтобы определить необходимый угол наклона ската крыши, нужно, в первую очередь, собрать постоянные нагрузки на кровлю. То есть получить суммарную нагрузку на 1 м2 от самого кровельного пирога и элементов крыши. Учитывается вес:
То есть получить суммарную нагрузку на 1 м2 от самого кровельного пирога и элементов крыши. Учитывается вес:
- внутренней и внешней обрешетки;
- стропил;
- утеплителя;
- внутренней отделки;
- кровельного покрытия;
- мансардных окон и световых тоннелей с окладом;
- водостоков;
- молниезащиты;
- оборудования, опирающегося на стропильную систему: спутниковых и телевизионных антенн, солнечных панелей и коллекторов, аэраторов;
- элементов безопасности кровли: снегозадержателей, переходных мостиков, лестниц.
Вес гидроизоляции и паробарьера обычно не учитывают, поскольку он пренебрежимо мал по сравнению с массой остальных элементов.
Для всех составляющих кровли рассчитывается их вес на 1 м2. Например, если обрешетка сделана из бруса 50×50 мм и закреплена с шагом 200 мм, то на 1 м2 будет приходиться всего четыре метровых бруска. Затем вес отдельных элементов суммируются, чтобы получить постоянную нагрузку на кровлю.
Расчет переменных нагрузок
Дальше нужно рассчитать временные нагрузки по нормативу СП 20.13330.2016 «Нагрузки и воздействия». Для частных домов это обычно только снеговая и ветровая нагрузка (разделы 10 и 11 документа).
Снеговая нагрузка на крышу
Снеговая нагрузка рассчитывается по формуле:
S0 =Sg·μ
где:
Sg — нормативный вес снегового покрова на горизонтальной поверхности. В зависимости от района строительства он равен:
| Снеговые районы | I | II | III | IV | V | VI | VII | VIII |
| Sg, кН/м2 | 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 |
Нормативный вес снегового покрова в разных районах
Сам район определяется по карте:
Если место строительства находится на границе двух снеговых районов, для него обычно берут бОльшую нормативную нагрузку, чтобы обеспечить кровле запас прочности на случай слишком снежной зимы.
Второй элемент формулы μ — это коэффициент, который зависит от формы крыши и ее уклона. Он позволяет перевести вес снегового покрова на горизонтальной плоскости в нагрузку на наклонном скате. Чем больше угол кровли, тем меньше μ, вплоть до 0.
Ветровая нагрузка на крышу
Ветровая нагрузка на крыши частных домов обычно существенно меньше снеговой. Но она все равно почти всегда превышает 10 кг/м2 и также зависит от угла наклона кровли, поэтому ее нельзя не учитывать.
Считают ветровую нагрузку wm по формуле:
wm = w0·k(ze)·c
где:
w0 — нормативная ветровая нагрузка. Как и снеговая, она зависит от места строительства:
| Ветровые районы | Ia | I | II | III | IV | V | VI | VII |
| w0, кПа | 0,17 | 0,23 | 0,3 | 0,38 | 0,48 | 0,6 | 0,73 | 0,85 |
Ветровой район определяют по карте:
Можно заметить, что единицы измерения ветровой нагрузки не в кН/м2, как у снеговой, а кПа. Это не ошибка, а просто разные обозначения одной и той же величины: 1 кПа = 1 кН/м2.
Это не ошибка, а просто разные обозначения одной и той же величины: 1 кПа = 1 кН/м2.
k(ze) — коэффициент, который зависит от высоты здания и типа местности.
Всего в СП 20.13330.2016 три типа местности:
- А — открытая местность: степи, пустыни, полупустыни, поля, побережья рек, озер и морей без преград, города с неплотной застройкой и высотой зданий меньше 10 м;
- В — местность, которая равномерно покрыта препятствиями высотой более 10 м: городские районы, леса.
- С — города с плотной застройкой, в которых есть здания высотой более 25 м.
Значения коэффициентов k(ze) для разной высоты приведены в таблице ниже:
| Высота ze, м | Тип местности | ||
| А | В | С | |
| ≤ 5 | 0,75 | 0,5 | 0,4 |
| 10 | 1,0 | 0,65 | 0,4 |
| 20 | 1,25 | 0,85 | 0,55 |
| 40 | 1,5 | 1,1 | 0,8 |
| 60 | 1,7 | 1,3 | 1,0 |
| 80 | 1,85 | 1,45 | 1,15 |
| 100 | 2,0 | 1,6 | 1,25 |
| 150 | 2,25 | 1,9 | 1,55 |
| 200 | 2,45 | 2,1 | 1,8 |
| 250 | 2,65 | 2,3 | 2,0 |
| 300 | 2,75 | 2,5 | 2,2 |
Последний параметр в формуле с — это аэродинамический коэффициент, который зависит от формы кровли и типа здания. Например, для обычных домов он считается по одной формуле, а для навесов — по другой.
Например, для обычных домов он считается по одной формуле, а для навесов — по другой.
Поскольку и снеговая, и ветровая нагрузка — переменные, при их сложении к меньшей нагрузке применяют коэффициент 0,9.
Теперь рассмотрим, как правильно рассчитать наклон крыши двух самых распространенных видов: односкатной и двухскатной.
Как рассчитать угол наклона крыши с одним скатом
Для односкатной крыши коэффициент μ равен:
- 1, если угол наклона ската кровли меньше 30°;
- 0, если этот угол больше 60°.
Промежуточные значения вычисляются по формуле:
μ = (60°−α)/(60°−30°)
где α — это уклон кровли.
Проще говоря, если крыша дома пологая (меньше 30°), то по строительным нормам на нее действует такая же снеговая нагрузка, как и на плоскую поверхность. Если же скаты крутые (больше 60°), то снеговую нагрузку можно вообще не учитывать в расчетах. Все значения углов между этими крайними точками оставляют маневр для подбора такого уклона ската, чтобы, с одной стороны, кровля не была слишком крутой, а с другой, чтобы скаты были наклонены достаточно для значимого уменьшения снеговой нагрузки.
Объясним на примере, как определить угол наклона крыши в градусах с учетом снеговой нагрузки. Возьмем такие исходные данные:
- Регион строительства — пригород Казани, это четвертый снеговой район с Sg = 2,0 кН/м2.
- Суммарная постоянная нагрузка на кровлю — 50 кг/м2.
- Стропильная система может выдержать нагрузку в 250 кг/м2.
Рассчитаем снеговую нагрузку при μ=1:
S0 =2·1=2 кН/м2
Чтобы перевести кН/м2 в кгс/м2, нужно умножить на 101,97. Итого снеговая нагрузка будет равна 203,94 кг/м2. Сложим с постоянной нагрузкой и получим 253,94 кг/м2 и это больше, чем может выдержать стропильная система, даже без учета ветровой нагрузки. Следовательно, угол нужно увеличить, чтобы уменьшить нагрузку.
Как высчитать угол наклона крыши в этом случае? Из несущей способности стропильной системы вычитаем постоянную нагрузку и получаем 200 кг/м2. Чтобы не пересчитывать минимальный уклон несколько раз, сразу учтем запас на ветровую нагрузку — 20 кг/м2, итого — 180 кг/м2.
Чтобы не пересчитывать минимальный уклон несколько раз, сразу учтем запас на ветровую нагрузку — 20 кг/м2, итого — 180 кг/м2.
Если заснеженную кровлю планируется чистить зимой, нужно сделать еще и запас на вес человека — 60 кг будет достаточно. Дело в том, что нормативный снеговой покров выпадает крайне редко — раз в несколько десятков лет. Поэтому, даже если человек будет весить больше, вреда крыше он не нанесет. Вес человека — эта точечная нагрузка, поэтому ее не распределяют по всей кровле, а учитывают в весе на 1 м2 «как есть».
После всех вычетов наш результат 120 кг/м2. Именно это — максимальная нагрузка, которую может давать снежная шапка на скате. Учитывая это, перед тем как рассчитать угол ската крыши, узнаем, каким должно быть μ:
2·101,97· μ =120 кгс/м2 → μ = 0,59
Теперь подставим это значение в формулу и рассчитаем минимальный угол наклона ската:
0,59 = (60°−α)/(60°−30°) → α = 42,3°
Итого, чтобы вписаться в ограничение по несущей способности, уклон скатов крыши нужно сделать равными 42,3° или больше. Лучше 45°, чтобы был запас прочности. При уклоне 45° снеговая нагрузка будет равна:
Лучше 45°, чтобы был запас прочности. При уклоне 45° снеговая нагрузка будет равна:
S0 =2·101,97·0,5=101,97 кН/м2
При расчете ветровой нагрузки для односкатной кровли коэффициент c зависит от преобладающего направления ветра.
Если ветер направлен в скат крыши, то коэффициент c берут из таблицы:
| Угол ската α | F | G | H | I | J |
| 0° | -1,8 | -1,3 | -0,7 | -0,5 | -0,5 |
| 15° | -0,9 | -0,8 | -0,3 | -0,4 | -1,0 |
| 0,2 | 0,2 | 0,2 | |||
| 30° | -0,5 | -0,5 | -0,2 | -0,4 | -0,5 |
| 0,7 | 0,7 | 0,4 | |||
| 45° | 0,7 | 0,7 | 0,6 | -0,2 | -0,3 |
| 60° | 0,7 | 0,7 | 0,7 | -0,2 | -0,3 |
| 75° | 0,8 | 0,8 | 0,8 | -0,2 | -0,3 |
Если ветер дует во фронтон, то используют другую таблицу:
| Угол ската α | F | H | G | I |
| 0° | -1,8 | -1,7 | -0,7 | -0,5 |
| 15° | -1,3 | -1,3 | -0,6 | -0,5 |
| 30° | -1,1 | -1,4 | -0,8 | -0,5 |
| 45° | -1,1 | -1,4 | -0,9 | -0,5 |
| 60° | -1,1 | -1,2 | -0,8 | -0,5 |
| 75° | -1,1 | -1,2 | -0,8 | -0,5 |
Минусы перед коэффициентами означают, что ветер не давит на кровлю, а, наоборот, приподнимает ее. Поэтому, если дом построен в районе, где ветер почти всегда дует в одном направлении, выгодно развернуть его фронтоном к воздушному потоку. Это снизит общую переменную нагрузку на конструкции.
Поэтому, если дом построен в районе, где ветер почти всегда дует в одном направлении, выгодно развернуть его фронтоном к воздушному потоку. Это снизит общую переменную нагрузку на конструкции.
В обоих случаях F, G, H, I и J — это обозначения для разных участков кровли, которые показаны на схеме:
На схеме — двускатная крыша, но ее можно использовать и для односкатной, совместив конек со стеной. На первой схеме конек совмещают с подветренной стеной, а на второй — с любой, это не повлияет на расчеты.
Теоретически, для каждого участка кровли расчет ветровой нагрузки нужно делать отдельно. И для больших промышленных, коммерческих и общественных зданий так и делают. Но для частных домов это смысла не имеет, поэтому на практике из строчки таблицы с нужным углом берется наибольший коэффициент (или наименьший, если он с минусом) и нагрузка считается по нему.
Для нашего примера коэффициент c нужно взять равным 0,7, а k(ze) — 0,65, поскольку дом строится в районе с неплотной и невысокой застройкой (тип местности В), а высота дома — больше 5 м, но меньше 10 м. Нормативная ветровая нагрузка — 0,3 кПа, поскольку Казань находится во втором ветровом районе. Следовательно, ветровая нагрузка будет равна:
Нормативная ветровая нагрузка — 0,3 кПа, поскольку Казань находится во втором ветровом районе. Следовательно, ветровая нагрузка будет равна:
wm = 0,3·0,65·0,7·101,97=13,92 кгс/м2
До того как посчитать угол наклона крыши исходя из максимальной снеговой нагрузки, мы закладывали запас на ветровую, равный 20 кг/м2. Поскольку расчетная нагрузка меньше этого запаса, пересчитывать наклон не нужно. Если на этом этапе ветровая нагрузка окажется больше, чем заложенное в расчеты значение, необходимо будет вернуться на несколько шагов назад и учесть уже расчетное число.
Как вычислить уклон кровли с двумя скатами
Уклон двускатной крыши рассчитывают почти так же, как и односкатной. Есть только несколько тонкостей при расчете снеговой нагрузки.
Поскольку у двускатной крыши есть конек, снег на ней часто распределяется неравномерно: ветер сдувает снег с одного ската, что уменьшает нагрузку на него, но сдутая часть оседает на втором скате и увеличивает нормативную толщину снегового покрова. В результате для одной крыши появляется сразу два коэффициента μ, как видно на схеме:
В результате для одной крыши появляется сразу два коэффициента μ, как видно на схеме:
Этот эффект проявляется, если уклон крыши 15° ≤ α ≤ 40°. В этом случае коэффициент μ нужно просто умножить на 1,25. То есть, он будет равен либо 1,25, если уклон меньше 30°, либо формула для его расчета немного изменится:
μ = 1,25·(60°−α)/(60°−30°),
Для частных домов μ с коэффициентом 0,75 обычно не берут. Во-первых, для этого нужно, чтобы ветер всегда дул только с одной стороны и никогда не менял направление зимой. Во-вторых, у симметричных двускатных кровель и стропильная система тоже симметричная, поэтому даже если в вашем регионе работает первое условие, в проекте все равно придется закладывать повышенную снеговую нагрузку для всей кровли.
Вторая особенность расчета нагрузки на двускатную кровлю и ее уклона касается относительно пологих крыш, у которых по коньку установлены аэрационные устройства или переходные мостики. Это не очень хорошее решение, поскольку расчет снеговой нагрузки в этом случае выполняется по схеме:
То есть, по аналогии с предыдущим случаем, коэффициент μ придется брать равным 1,4. Либо делать кровлю, уклон которой не будет попадать в диапазон: 10° ≤ α ≤ 30° — именно в нем работает эта схема.
Либо делать кровлю, уклон которой не будет попадать в диапазон: 10° ≤ α ≤ 30° — именно в нем работает эта схема.
При расчете ветровой нагрузки никаких особенностей у двускатной крыши нет — для частных домов все считается так же, как и для односкатной.
Как рассчитать уклон кровли под конкретное кровельное покрытие
На допустимый угол кровли влияет не только расчетная нагрузка, но и кровельное покрытие. Большинство кровельных материалов нельзя укладывать на очень пологие кровли, у некоторых есть ограничения и по максимальному углу наклона.
Поэтому после расчета минимального угла по нагрузке, нужно проверить, можно ли на скат с таким уклоном монтировать выбранный вид кровельного покрытия. Эти значения для популярных материалов приведены в таблице:
| Вид кровельного покрытия | Минимальный уклон ската кровли | Максимальный уклон ската кровли |
| Шифер | 25° | 45° |
| Ондулин | 5° | нет |
| Битумная черепица | 6° | нет |
| Фальцевая кровля | 7° | нет |
| Керамическая черепица | 22° (классика) и 30° (бобровый хвост) | 60° |
| Металлочерепица | 9° | нет |
| Профнастил | 8-10° | нет |
| Цементно-песчаная черепица | 22-30° | 60° |
Большинство кровельных материалов можно укладывать на скаты с меньшим уклоном, чем указано в таблице. Но это дорого: протечки в этом случае практически гарантированы, поэтому нужны большие нахлесты и дополнительная герметизация кровли. И это не просто больше герметика в стыках: под кровельным покрытием необходимо, фактически, сделать вторую кровлю из рулонных битумных материалов или качественной гидроизоляционной мембраны с проклеенными стыками.
Но это дорого: протечки в этом случае практически гарантированы, поэтому нужны большие нахлесты и дополнительная герметизация кровли. И это не просто больше герметика в стыках: под кровельным покрытием необходимо, фактически, сделать вторую кровлю из рулонных битумных материалов или качественной гидроизоляционной мембраны с проклеенными стыками.
Кроме того, у профнастила, как у самонесущего кровельного материала, тоже есть своя максимальная допустимая нагрузка в зависимости от марки и расстояния между брусками обрешетки. Это значит, что если планируется перекрытие кровли этим материалом, то при расчете снеговой и ветровой нагрузке нужно смотреть не только на несущую способность стропильной системы, но и учитывать, выдержит ли такой вес сам кровельный материал.
Если дом уже построен, то есть два способа, как вычислить угол ската крыши:
- Инструментальный с помощью уклономеров и угломеров.
- Расчетный, который опирается на базовую геометрию и измерение двух катетов прямоугольного треугольника.

Если дом только проектируется, то нужно знать, как правильно рассчитать уклон крыши в зависимости от нагрузки на скаты. Для этого нужно вычислить:
- Постоянные нагрузки на кровлю (вес кровельного пирога, дополнительного оборудования, мансардных окон, внутренней отделки и т.д.). Они не зависят от угла наклона кровли.
- Переменные нагрузки (снеговую и ветровую). Они прямо зависят от уклона ската крыши, поэтому по ним и вычисляют минимальный угол.
Кроме нагрузок при расчете уклона кровли нужно учитывать тип кровельного покрытия. У всех кровельных материалов есть ограничения по минимальному углу наклона, у некоторых ограничен и максимальный.
Угол уклона пандуса
Основным нормативным документом для определения уклона пандуса и его длины в РФ является СП 59.13330.2012 «Доступность зданий и сооружений для маломобильных групп населения» С Изменением №1 — актуализированная версия СНиП 35-01-2001.
Допустимые значения угла наклона пандуса
— Допустимый угол уклона пандуса должен быть не круче 1:20 (5%), а максимальная высота одного подъема (марша) пандуса не должна превышать 0,8 м.
— При перепаде высот пола на путях движения 0,2 м и менее допускается увеличивать уклон пандуса до 1:10 (10%)
— На временных сооружениях или объектах временной инфраструктуры допускается максимальный уклон пандуса 1:12 (8%) при условии, что подъем по вертикали между площадками не превышает 0,5 м, а длина пандуса между площадками — не более 6,0 м.
— Пандусы при перепаде высот более 3,0 м и расчетной длиной более 36 м следует заменять лифтами, подъемными платформами и т.п
— В соответствии с приказом Минстроя России №750/пр от 21 октября 2015 г. «Об утверждении изменений №1 к СП 59.13330.2012 «Доступность зданий и сооружений для маломобильных групп населения» «При проектировании реконструируемых, подлежащих капитальному ремонту и приспосабливаемых существующих зданий и сооружений уклон пандуса принимается в интервале от 1:20 (5%) до 1:12 (8%)».
Что обозначают цифры
1:10 — 10% — один к десяти, т.е. при перепаде высот в 1 м, длина пандуса должна быть 10 м, при высоте 0,5 м — длина пандуса должна быть 5 м и т.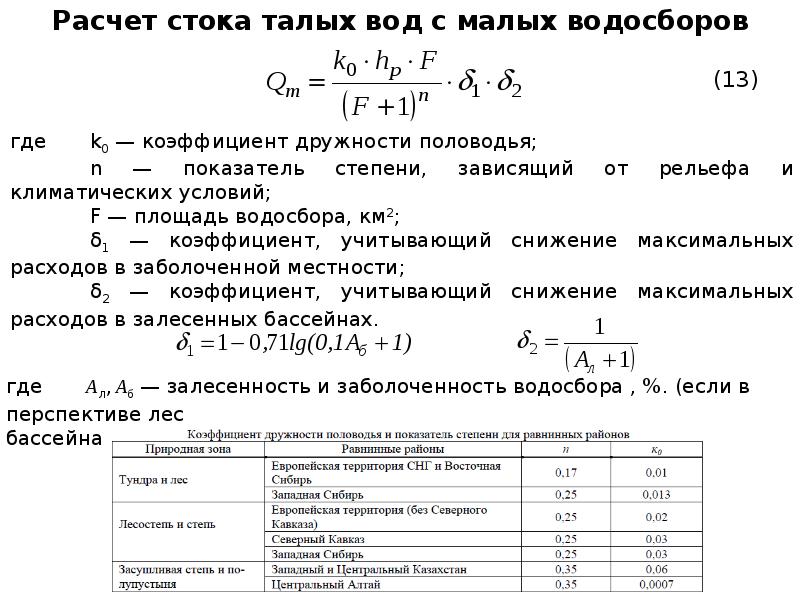 д.
д.
В этом случае угол уклона пандуса будет соответствовать 5,7 градусам.
1:12 — 8% — один к двенадцати, т.е. при перепаде высоты в 1 м, длина пандуса должна быть 12 м, при высоте 0,5 м — длина пандуса должна быть не менее 6 метров и т.д.
Угол уклона пандуса будет равен 4,8 градусам.
1:20 — 5% — один к двадцати, т.е. при перепаде высот 1 м, длина пандуса должна быть 20 м, при высоте 0,5 м — 10 м.
Угол уклона пандуса будет равен 2,9 градусам.
Какой длины делать пандус?
|
|
|||
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Зеленый — допустимые значения, красный — недопустимые.
Если Вам необходимо самостоятельно рассчитать угол уклона пандуса, зная его длину и высоту, то необходимо воспользоваться следующей формулой
arcsin(h/L), где h — высота, L — длина.
Для этого
воспользуйтесь инженерным калькулятором
Примеры внедрений
|
На изображениях конических элементов деталей размеры могут быть проставлены различно: диаметры большего и меньшего оснований усеченного конуса и его длина; угол наклона образующей (или угол конуса) или величина конусности и диаметр основания, длина и т.п. Блок: 1/3 | Кол-во символов: 271 Уклон Плоские поверхности деталей, расположенные наклонно, обозначают на чертеже величиной уклона. Как подсчитать эту величину, покажем на примере. Клин, изображенный на рис. 6.40, я, имеет наклонную поверхность, уклон которой нужно определить. Рис. 6.40. Определение величины уклона На чертеже уклоны указывают знаком и отношением двух чисел, например 1:50; 3:5. Если требуется изобразить на чертеже поверхность определенного уклона, например 3:20, вычерчивают прямоугольный треугольник, у которого один из катетов составляет три единицы длины, а второй – 20 таких же единиц (рис. 6.41). Рис. 6.41. Построение уклонов и нанесение их величин При вычерчивании деталей или при их разметке для построения линии по заданному уклону приходится проводить вспомогательные линии. Рис. 6.42. Построение линии по заданному уклону Вершина знака уклона должна быть направлена в сторону наклона поверхности детали. Знак и размерное число располагают параллельно направлению, по отношению к которому задан уклон. |
Калькулятор Уклонов найти наклон линии
Может быть, вы знакомы с вопросом «как рассчитать уклон»! Наклон является важной концепцией в математике, которая обычно используется в базовом или расширенном графике, таком как линейная регрессия; говорят, что наклон является одним из основных чисел в линейной формуле.
Ну что ж, самое главное – команда онлайн-калькуляторов предлагает еще один образовательный инструмент, известный как «калькулятор уклонов», который помогает найти неопределенный уклон с помощью простой формулы уклона. В этом посте мы решили обсудить расчет уклона, как найти уклон, что такое формула уклона, и все, что вам нужно знать о уклоне!
Итак, начнем с «определения уклона».
Что такое склон?
Определение уклона очень просто; говорят, что это мера разницы в положении между двумя точками на линии. Согласно математике, если линия построена на двухмерном графике, то наклон – это то, что показывает, насколько линия движется вдоль оси x и оси y между этими двумя точками. Да, найти уклон становится легко с помощью нашего надежного калькулятора уклонов – этот инструмент использует простое уравнение уклона, чтобы найти уклон.
Согласно математике, если линия построена на двухмерном графике, то наклон – это то, что показывает, насколько линия движется вдоль оси x и оси y между этими двумя точками. Да, найти уклон становится легко с помощью нашего надежного калькулятора уклонов – этот инструмент использует простое уравнение уклона, чтобы найти уклон.
Формула уклона:
Наклон (м) = ΔY / ΔX
В этом уравнении наклона;
M = уклон
ΔY = (y₂ – y₁)
ΔX = (x₂ – x₁)
Kалькулятор Yклонов По калькулятору онлайн:
К счастью, вы можете найти наклон или градиент между двумя точками в декартовой системе координат с помощью нашей точки расчет уклона. Да, это калькулятор уклонов помогает вычислить уклон (из точек) для данного ввода. Проще говоря, эта точка онлайн калькулятор уклонов r работает как «искатель склона». Хорошо, заполните поля вышеупомянутой находки калькулятор наклона, чтобы найти наклон линии.
Наш Pасчет Yклона работает:
Калькулятор формулы наклона очень удобен в использовании; он использует простую формулу для наклона в поиске наклона линии.
Вы должны придерживаться указанных шагов для наклона между двумя точками:
- В приведенном выше калькуляторе вы можете видеть поля для X1, Y1, X2 и Y2 соответственно!
- Прежде всего, вы должны ввести значения четырех координат
- Сразу после этого вы должны нажать кнопку расчета
- После этого вы получите пять выходных значений, включая наклон, угол наклона, расстояние, изменение X и изменение Y
К счастью, вы узнали, как найти уклон, используя простой уклон линейной формулы.
Как найти наклон линии?
Вы можете найти наклон линии, сравнивая любые 2 точки на линии. Точка называется значением X и Y декартовой координаты на сетке. Склон; представленный как m, его можно найти, используя формулу наклона:
Формула уклона: m = ((y2 – y1)) / ((x2 – x1))
Например:
Линия проходит через точки (3, 2) и (7, 5), как найти наклон линии?
Решение:
m = ((5 – 2)) / ((7 – 3))
m = ((3)) / ((4))
Как найти расстояние между 2 точками?
Формула для определения расстояния (D) между двумя разными точками:
Расстояние (d) = √ (〖ΔX〗 ^ 2 + 〖ΔY〗 ^ 2)
Где – 〖ΔX〗 ^ 2 = 〖(x₂ – x₁)〗 ^ 2 и 〖ΔY〗 ^ 2 = 〖(у₂ – у₁)〗 ^ 2
Как конвертировать наклон в угол?
Вы можете найти угол наклона линии в градусах от обратного тангенса наклона (м). Кроме того, вы можете использовать простой калькулятор касательной линии, чтобы скрыть наклон к ангелу.
Кроме того, вы можете использовать простой калькулятор касательной линии, чтобы скрыть наклон к ангелу.
Формула это:
θ = загар-1 (м)
ИЛИ θ = арктан (ΔY / ΔX)
Куда;
м = уклон
θ = угол наклона
Например:
Если наклон равен 5, угол наклона в градусах равен tan-1 (5).
Как конвертировать угол в наклон?
Вы также можете преобразовать угол в градусах в уклон. Просто все, что вы должны помнить, это то, что наклон равен тангенсу угла.
Уравнение:
m = tan (θ)
Например: если угол = 90, то наклон равен tan (90).
Слова по калькулятору онлайн:
К счастью, вы узнали, как найти склон. Удивительно то, что вам не нужно запоминать эти формулы, вам просто нужно ввести четыре координаты в калькуляторе выше, чтобы найти наклон, угол наклона, расстояние, изменение в X и изменение в Y, соответственно!
Other Languages: Slope Calculator, Steigung Berechnen, 勾配計算, Calcul Pente, Calculo De Inclinação, Calcular Pendiente, Calcolo Pendenza, Výpočet Sklonu, Kattokaltevuus Laskuri, Eğim Hesaplama, Kalkulator Nachylenia, Kalkulator Kemiringan.
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}}
{{addToCollection.description.length}}/500
{{l10n_strings.TAGS}}
{{$item}}
{{l10n_strings.PRODUCTS}}
{{l10n_strings.DRAG_TEXT}}
{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings. LANGUAGE}}
LANGUAGE}}
{{$select.selected.display}}
{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}}
{{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}}
как узнать угол наклона ската в градусах, как рассчитать угол стропил двухскатной крыши, узнать и высчитать
Единицы измерения угла ската
Из школьного курса геометрии все знают, что величина любого угла измеряется в градусах. Уклон кровли в этом случае – не исключение. Но необходимо обозначить, что в технической литературе, в ГОСТах и справочниках встречают и другие единицы измерения. А именно: проценты и отношения сторон.
Уклон кровли в этом случае – не исключение. Но необходимо обозначить, что в технической литературе, в ГОСТах и справочниках встречают и другие единицы измерения. А именно: проценты и отношения сторон.
В первую очередь надо обозначить, что подразумевают под углом ската крыши. На фото ниже он обозначен латинской буквой альфа.
Угол наклона ската кровли Источник remontik.org
В строительной сфере крыши с углом наклона выше 50° встречаются редко. К ним можно отнести башенки в готическом стиле или нижние скаты мансардных кровель. В основном максимальный параметр – 45°.
Что касается двух других единиц измерения, то отношение сторон – это так называемая упрощенная дробь. В ее основе лежат два размера: высота крыши, на фото она обозначена буквой «Н», и проекцией ската, обозначенная буквой «L». Соотношение должно быть таким: Н/L.
Добавим, что проекция длины ската – это, по сути, половина ширины дома, если крыша двускатная симметричная, или полная ширина, если крыша односкатная. При этом угол наклона так и пишется дробью, к примеру, 1:3.
При этом угол наклона так и пишется дробью, к примеру, 1:3.
В некоторых конструкций обозначение дробью неудобно. К примеру, если она выглядит вот так: 4:13. Поэтому используют процентное исчисление. Оно рассчитывается таким образом:
4:13х100=30,77%
Уклон кровли в процентах и градусах используется профессиональными строителями чаще, чем отношение сторон, потому что такое обозначение применяется в справочниках и технической литературе. То есть это чисто технические единицы измерения. Хотя перевести из одной единицы измерения в другую не сложно. На фото ниже показан перевод из градусов и отношении я сторон и наоборот.
Пропорции соотношения градусов к размерам крыши Источник obustroeno.com
Если есть необходимость перевести градусы в проценты, то, исходя из рисунка выше, можно сделать несколько математических выкладок. За 100% берется угол, равный 45°. Теперь можно найти, сколько градусов в одном проценте. Для этого надо:
45/100=0,45°. Переводим в минуты, получается 27’. То есть 1% – это 27 градусных минут.
То есть 1% – это 27 градусных минут.
Можно подойти к решению поставленной задачи с обратной стороны. То есть перевести градусы в проценты. Здесь обратное соотношение:
100/45=2,22%
Получается так, что в одном градусе 2,22%.
На нашем сайте Вы можете найти контакты строительных компаний, которые предлагают услугу расчета, монтажа и ремонта кровли. Напрямую пообщаться с представителями можно посетив выставку домов «Малоэтажная Страна».
Зависимость угла наклона ската и типа кровельного материала
Вышу уже говорилось о двух разновидностях кровель: плоские и наклонные. Но надо отметить, что у плоских кровель тоже есть свой угол, который варьируется в диапазоне 0-5°. Скатные крыши делятся на две подгруппы (деление условное):
- с небольшим уклоном – от 6 до 30°;
- с крутым уклоном – больше 30°.
Распределение кровельных материалов по крутизне ската Источник belhouse.by
У каждого вида кровельных конструкций есть свои преимущества и недостатки. К примеру, плоские – это небольшая площадь покрытия, что позволяет сэкономить на кровельном материале (его количестве). Но при этом такая конструкция потребует проведения усиленной гидроизоляции. Крутые скаты – это беспроблемное схождение атмосферных осадков, но высокая парусность конструкции, что потребует от ее сооружения усиления стропильной системы.
К примеру, плоские – это небольшая площадь покрытия, что позволяет сэкономить на кровельном материале (его количестве). Но при этом такая конструкция потребует проведения усиленной гидроизоляции. Крутые скаты – это беспроблемное схождение атмосферных осадков, но высокая парусность конструкции, что потребует от ее сооружения усиления стропильной системы.
Учитывая это, необходимо строго подходить к выбору кровельного материала. Их производители обязательно информируют потребителей, при каком минимальном уклоне кровли их можно использовать. На фото ниже показана диаграмма распределения кровельных материалов по углам скатов.
Как видно из диаграммы, на плоских крышах обычно используют рулонные материалы в виде рубероида или толи. Хотя нет никаких противопоказания применения листовых или плитных изделий: шифер, профнастил, листовое железо, собираемое фальцовым способом. А вот штучный кровельный материал лучше на крышах крутизною меньше 15° не использовать. Есть высокая вероятность проникновения воды через стыки элементов покрытия.
Значение угла кровли в градусах и процентах по отношению к типу кровельного материала Источник remotvet.ru
Что на него влияет
В зависимости от величины уклона скатов крыши зависит особенность ее эксплуатации.
Принято выделять 4 типа крыш: высокие — с углом в 45–60 градусов; скатные — с наклоном от 30 до 45 градусов; пологие — с углом уклона 10–30 градусов; плоские — с углом 10 градусов и меньше.
На выбор величины этого параметра оказывают влияние, в первую очередь, природные факторы, которые характерны для данной местности.
Ветровая нагрузка
Сильный ветер самое большое давление оказывает на кровли высокие. Потому что такие кровли из-за большого угла наклона имеют очень большую площадь. У большой площади поверхности очень высока парусность. Соответственно, очень велика нагрузка на всю конструкцию стропильной системы. И если вы решили устраивать именно высокую кровлю с очень большим уклоном, то следует позаботиться и об очень прочном основании. Однако в районах, где преобладают сильные ветра, небезопасно устраивать и крыши плоские. При таком типе кровли на нижнюю часть ската будет оказываться повышенное давление при сильном ветре. И если крепление кровли будет ослабленным, может произойти срыв всей конструкции. Поэтому в районах, где сильные ветра бывают часто, рекомендуется устраивать скатные кровли с величиной наклона 25–30 градусов. Если же сила ветра невелика, то величина уклона крыши может равняться 30–45 градусов.
Однако в районах, где преобладают сильные ветра, небезопасно устраивать и крыши плоские. При таком типе кровли на нижнюю часть ската будет оказываться повышенное давление при сильном ветре. И если крепление кровли будет ослабленным, может произойти срыв всей конструкции. Поэтому в районах, где сильные ветра бывают часто, рекомендуется устраивать скатные кровли с величиной наклона 25–30 градусов. Если же сила ветра невелика, то величина уклона крыши может равняться 30–45 градусов.
Нагрузка снеговая
Если в той местности, где строится дом, в холодное время года снегопад обильный, то следует строить кровлю с большим углом уклона. В этом случае высокая крыша вне конкуренции. На кровлях с большим уклоном снег не задерживается. Именно по этой причине во всех северных странах кровли на зданиях очень высокие (Швеция, Финляндия, Норвегия и пр.). Чем меньше угол уклона кровли, тем дольше выпавший снег будет находиться на скатах. Тем больший вес будет воздействовать на всю конструкцию. Если конструкция стропильной системы сделана с большим запасом прочности, то некоторый слой снега на крыше — это неплохо. Он обеспечивает небольшую дополнительную теплоизоляцию. Однако, если конструкция стропильной системы сооружения на большую нагрузку не рассчитана, то могут быть большие проблемы.
Если конструкция стропильной системы сделана с большим запасом прочности, то некоторый слой снега на крыше — это неплохо. Он обеспечивает небольшую дополнительную теплоизоляцию. Однако, если конструкция стропильной системы сооружения на большую нагрузку не рассчитана, то могут быть большие проблемы.
Конструктивные особенности крыши в зависимости от угла наклона
Если в проекте дан уклон крыши, то рассчитать ее высоту не составит труда. А этот параметр – один из самых важных, потому что он определяет высоту конька. Этот элемент кровельной конструкции – точка отправления в сооружении крыши в целом. Потому что при строительстве сначала выставляют уровень расположения конька, и уже под него режут пиломатериал: опорные стойки. Отсюда же рассчитывают длину стропильных ног.
Сложность расчета заключается в том, что не все помнят тригонометрию, формулы которой используются для расчетов длин элементов кровельного сооружения. В основе формул лежат тригонометрические функции: синус, косинус, тангенс, катангенс.
К примеру, как определить высоту конька (соответственно и крыши) через синус и тангенс:
sin α = H/S, где «S» – это длина ската. Соответственно высота конька будет равна: Н=S x sin α.
tg
α =H/L, то есть Н=lxtgα
Точно также можно определить длину ската, или, зная оба параметра, можно рассчитать угол наклона крыши. Все параметры конструкции взаимосвязаны, так что, зная два из них, можно определить третий.
Это может быть интересно!
В статье по следующей ссылке читайте про вентиляцию подкровельного пространства.
Кстати, определяя параметры крыши, можно обойтись и без угла наклона. Для этого используется формула Пифагора. Вот ее формула:
S2=H2+L2
Меняя местами значения, находится необходимая величина.
У Вас может возникнуть вопрос, связанный со значением величин тригонометрических функций. Они в свободном доступе есть, но чтобы Вы их не искали на просторах интернета и не тратили свое время, предлагаем таблицу:
Они в свободном доступе есть, но чтобы Вы их не искали на просторах интернета и не тратили свое время, предлагаем таблицу:
Значения тригонометрических функций от величины угла Источник remont-kvartiri.livejournal.com
Добавим, что тригонометрические функции упрощают проведения расчетов кровельных конструкций. Если правильно ими пользоваться и уметь набрасывать на бумаге эскизы крыш (имея воображение в плане конструктивного расположения ее элементов), то можно легко рассчитать размеры каждого элемента.
Это касается не только одно- или двускатных сооружений. Также легко можно будет рассчитать и элементы вальмовых или мансардных крыш. Просто придется разбить их сложные конструкции на простые.
Расчет углов уклона кровель по типам
Расчет угла наклона односкатной крыши
Односкатная кровля является одной из самых популярных и, одновременно, одной из самых легких для расчета. Фактически — наш калькулятор рассчитывет именно ее, так как более сложные кровли (например, угол наклона двускатной крыши) требуют разбивки элементов кровли на отдельные скаты и просчета каждого из них.
При расчете наклона односкатной кровли и расчете длины и угла ската крыши обязательно учитывайте свесы! Посчитать их можно задавай данные не самого ската, а высоту и проекцию кровли именно вместе со свесами.
Материалы и углы для односкатных кровель
- крыша из рубероида – 5-10 градусов
- из профнастила – от 8 до 20 градусов
- из металлочерепицы – 20-30 градусов
- из шифера – 20-35 градусов
- для фальцевой кровли необходим наклон 18-30 градусов
Расчет угла наклона двускатной крыши
Посчитать двускатную кровлю уже сложнее, чем посчитать угол наклона односкатной кровли. В случае для двух скатов необходимо рассчитывать на нашем калькуляторе уже каждый из скатов индивидуально, а для расчета материала лучше применть калькулятор кровли, т.к. расположение материала и его размеры могут гулять.
Расчет угла наклона вальмовой кровли
В свою очередь расчет вальмовой кровли еще сложнее чем расчет угла двускатной кровли. Вам необходимо не просто разбить и считать угол каждого ската отдельно, но и учитывать что углы для вальмовой кровли различаются.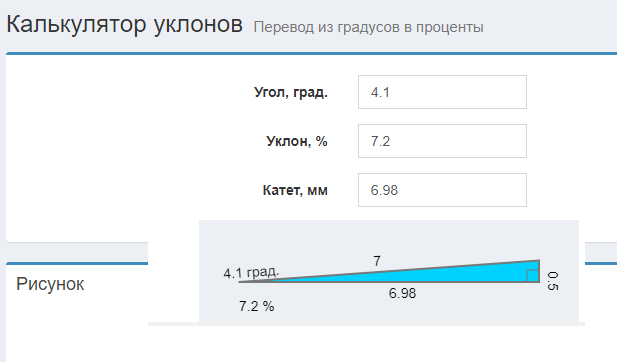
Для вальмовой кровли так же особенно нужн учесть гуляющие размеры обрешетки, поэтому при расчете Вашей реальной кровли углы вальмовой кровли пусть немного, но будут различаться!
Влияние угла наклона на объем помещения мансарды
Если дом возводится с мансардой, то угол наклона скатов приобретает прикладное значение. И здесь соотношение прямое, то есть чем больше угол, тем больше объем мансарды. Чтобы было понятно, на фото ниже это хорошо видно.
Соотношение угла наклона скатов к объему мансардного помещения Источник legkovmeste.ru
Приведем пример, основанный на верхнем рисунке. Здесь четко видно, что высота помещения зависит от параметров наклона крыши. При этом надо учитывать, что оптимальная высота не должна быть меньше 2,5 м. А значит, угол наклона скатов мансарды минимально должна быть 25°. Но обратите внимание, что при таком расположении элементов кровли не учтен объем помещения. То есть ширина комнаты не будет больше 3 м. Это притом, что ширина дома – 10 м.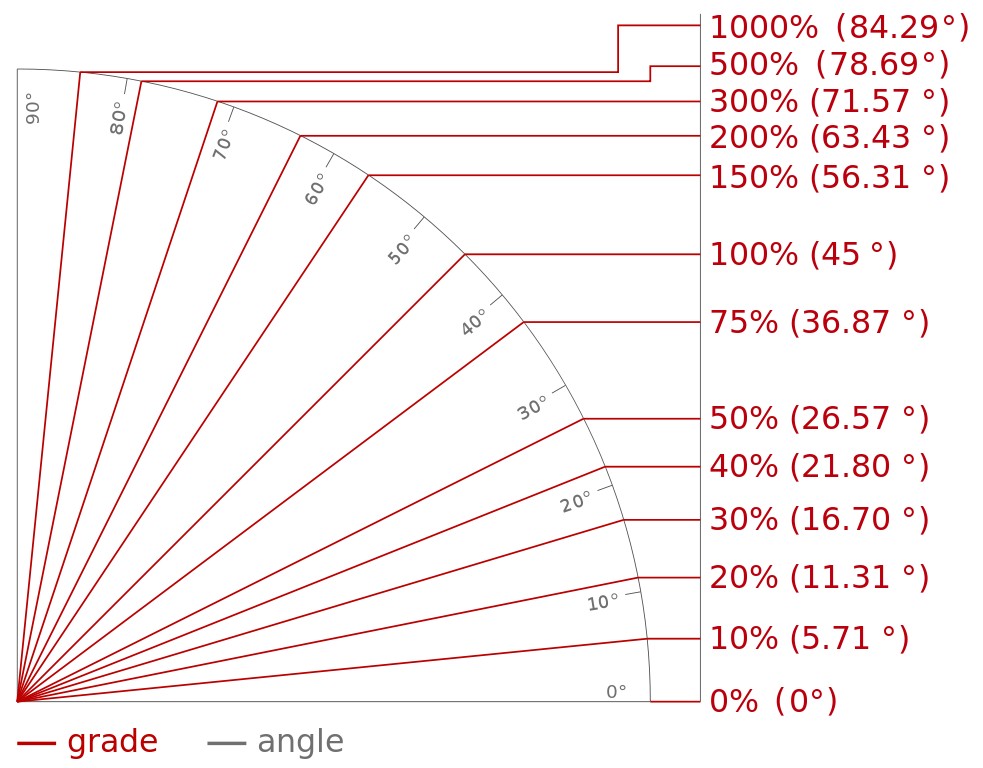 Получается, что используется всего лишь 30% от пространства.
Получается, что используется всего лишь 30% от пространства.
А значит, надо увеличивать значение угла. И чем больше он, тем больше полезная площадь мансарды. Но здесь есть обратная сторона медали. Увеличивая угол, увеличивается высота конька. А это расходы стройматериалов на возведение крыши, плюс увеличение парусности конструкции. Поэтому очень важно найти золотую середину. К примеру, 40° практически решают все проблемы.
Чтобы отойти от этих проблем раз и навсегда, строители давно применяют совершенно другую конструкцию. Она сложна и в сооружении, и в проведении расчетов, но этот вариант решает проблему полезной площади помещения, не увеличивая высоту крыши.
Конструкция мансардной крыши Источник ok.ru
Критерии выбора
Выбор уклонности основывается на инженерном расчете, учитывающем климатические условия зоны, где ведется строительство, характеристики кровельного покрытия и несущую способность стропильного каркаса. Чтобы конструкция получилась надежной, необходимо принимать во внимание следующие критерии:
- Ветровая нагрузка.
 Чем круче кровля, тем сильнее ее парусная способность. Поэтому в регионах с сильным, порывистым ветром предпочтительнее более пологие кровельные конструкции. Хотя с другой стороны, с низкоуклонных скатов ветром может срывать гидроизоляционный материал.
Чем круче кровля, тем сильнее ее парусная способность. Поэтому в регионах с сильным, порывистым ветром предпочтительнее более пологие кровельные конструкции. Хотя с другой стороны, с низкоуклонных скатов ветром может срывать гидроизоляционный материал. - Снеговая нагрузка. Чем больше снеговая нагрузка, тем более крытыми делают скаты. Угол наклона кровли 40-45 градусов обеспечивает самостоятельный сход снега с поверхности кровельного материала.
- Характеристики финишного покрытия. У каждого покрытия для возведения кровли существует оптимальный уклон, который необходимо учитывать при проектировании конструкции.
- Несущая способность каркаса. Чем меньше сечение элементов каркаса и больше расстояние между ними, тем выше круче должен быть скат, чтобы выдержать снеговую нагрузку.
Влияние уклона на шаг обрешетки
Вес низкоуклонной и среднеуклонной крыши
Формула уклона
— что такое формула уклона? Уравнение, примеры
Формула уклона используется для расчета наклона или крутизны линии. Он находит применение при определении наклона любой линии путем нахождения отношения изменения по оси у к изменению по оси х. Наклон линии определяется как изменение координаты «у» по отношению к изменению координаты «х» этой линии.
Он находит применение при определении наклона любой линии путем нахождения отношения изменения по оси у к изменению по оси х. Наклон линии определяется как изменение координаты «у» по отношению к изменению координаты «х» этой линии.
Что такое формула уклона?
Формула наклона относится к формуле, используемой для расчета крутизны линии и определения степени ее наклона.Для вычисления наклона линий можно использовать координаты x и y точек, лежащих на линии. Другими словами, это отношение изменения по оси у к изменению по оси х.
Формула уклона
Формула для расчета наклона дается как,
м = (y 2 — y 1 )/(x 2 — x 1 ) = Δy/Δx
, где m — наклон линии, x 1 , x 2 — координаты по оси X, а y 1 , y 2 — координаты по оси Y.
Вывод формулы уклона
Координаты x и y линии используются для расчета наклона линии. Чистое изменение координаты y равно Δy, а чистое изменение координаты x равно Δx. Таким образом, изменение координаты y по отношению к изменению координаты x можно записать как
Чистое изменение координаты y равно Δy, а чистое изменение координаты x равно Δx. Таким образом, изменение координаты y по отношению к изменению координаты x можно записать как
.
м = Δy/Δx
где
- м — склон
- Δy — изменение координаты y
- Δx — изменение координаты x
Мы знаем, что тангенс θ также является наклоном линии, где θ — это угол, образуемый линией с положительным направлением оси x.
А, tanθ = высота/основание
Поскольку высота/основание между любыми двумя заданными точками = (y 2 — y 1 )/(x 2 — x 1 )
Таким образом, уравнение наклона: m = tanθ = Δy/Δx
Из графика наблюдаем:
- Δу = (у 2 — у 1 )
- Δx = (х 2 — х 1 )
Таким образом, формула уклона имеет вид: Уклон = m = (y 2 — y 1 )/(x 2 — x 1 )
Уравнение наклона
Как мы обсуждали в предыдущем разделе, формулу наклона можно использовать для определения наклона любой линии. Таким образом, уравнение, которое можно использовать для нахождения этого наклона, можно записать как
Таким образом, уравнение, которое можно использовать для нахождения этого наклона, можно записать как
.
m = рост/бег = tanθ = Δy/Δx = (y 2 — y 1 )/(x 2 — x 1 )
где,
- м — склон
- Δy — изменение координаты y
- Δx — изменение координаты x
- θ — угол, образуемый линией с положительной осью x
Кроме того, уравнение наклона любой линии с использованием уравнения линии может быть задано как
у = мх + б
где,
- м — уклон линии
- b — точка пересечения по оси y линии
.
Рассмотрим применение формулы наклона в следующих решенных примерах.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Забронируйте бесплатный пробный урок
Примеры использования формулы уклона
Пример 1: Найдите наклон линии с координатами (2,9) и (4,1)?
Решение:
Найти: Наклон линии с координатами (2,9) и (4,1)
Дано, (x 1 , y 1 ) = (2, 9) и (x 2 , y 2 ) = (4, 1)
Формула наклона m = (y 2 — y 1 )/(x 2 — x 1 )
м = (1 − 9)/(4 − 2)
м = -8/2 = -4
Ответ: Наклон данной линии = -4
Пример 2: Определите значение b, если наклон линии, проходящей через точки (b, 7) и (8, -5), равен 6.
Решение:
Найти: значение b
Дано, Наклон = m = 6, Точки: (x 1 , y 1 ) = (b, 7) и (x 2 , y 2 ) = (8, -5)
Мы знаем, что Уклон (м) = (y 2 — y 1 )/(x 2 — x 1 )
6 = (-5-7)/(8-б)
6 = (-12)/(8-б)
-2= (8-б)
-2-8 = -б,
b = 10
Ответ: Значение b = 10.
Пример 3: Если угол, образуемый линией с положительной осью y, равен 30°, то каково значение наклона линии?
Решение:
Найти: наклон линии
Дано: Угол, образованный линией с положительной осью y = 30°
Мы знаем, что если линия образует угол 30° с положительной осью y, то она образует угол 120° с положительной осью x.Следовательно, значение наклона линии равно tan120° = -√3
Ответ: Значение наклона линии = -√3
Часто задаваемые вопросы о формуле склона
Что такое формула уклона в геометрии?
В геометрии формула наклона определяется как формула для вычисления наклона любой линии путем нахождения отношения изменения по оси Y к изменению по оси X.
Что означает m в формуле уклона?
В формуле уклона m означает уклон, который рассчитывается как m = (y 2 — y 1 )/(x 2 — x 1 ) = Δy/Δx
Для чего используется формула уклона?
Формула наклона используется для расчета крутизны линии, а координаты линий x и y используются для того же.Мы знаем, что наклон линии является одной из наиболее важных характеристик линии, поскольку он помогает измерить скорость изменения.
Как рассчитать уклон, используя формулу уклона?
Наклон линии можно рассчитать по следующим формулам:
Когда заданы координаты:
- Шаг 1: Найдите координаты линии.
- Шаг 2: Подставьте их значения в формулу (m) = (y 2 — y 1 )/(x 2 — x 1 )
Когда задан угол:
- Шаг 1: Определите угол, образуемый с осью.
- Шаг 2: Подставьте значение в формулу, m = tanθ
Что такое уравнение наклона линии?
Уравнение наклона любой линии можно рассчитать по следующей формуле:
м = подъем/бег = tanθ = Δy/Δx = (y 2 — y 1 )/(x 2 — x 1 )
где,
- м — склон
- Δy — изменение координаты y
- Δx — изменение координаты x
- θ — угол, образуемый линией с положительной осью x
Уравнение наклона с использованием уравнения прямой задается как y = mx + b, здесь m — это наклон, а b — точка пересечения с осью y.
Калькулятор уклона
|
По определению наклон или уклон линии описывает ее крутизну, наклон или уклон. Где м — уклон |
Если известны 2 точки
Если известна 1 точка и наклон
Уклон, иногда называемый в математике градиентом, представляет собой число, которое измеряет крутизну и направление линии или участка линии, соединяющей две точки, и обычно обозначается как м .Как правило, крутизна линии измеряется абсолютным значением ее наклона, м . Чем больше значение, тем круче линия. Имея м , можно определить направление линии, которую описывает м на основе ее знака и значения:
- Линия увеличивается и идет вверх слева направо, когда m > 0
- Линия убывает и идет вниз слева направо, когда m < 0
- Линия имеет постоянный наклон и является горизонтальной, когда m = 0
- Вертикальная линия имеет неопределенный наклон, так как в результате получится дробь со знаменателем 0.
 См. приведенное ниже уравнение.
См. приведенное ниже уравнение.
Уклон — это, по сути, изменение высоты по сравнению с изменением горизонтального расстояния, и его часто называют «подъемом над уклоном». Он применяется в градиентах в географии, а также в гражданском строительстве, например, при строительстве дорог. В случае дороги «подъем» — это изменение высоты, а «пробег» — это разница в расстоянии между двумя фиксированными точками, если расстояние для измерения недостаточно велико, чтобы кривизна земли была рассматривается как фактор.Наклон представлен математически как:
В приведенном выше уравнении y 2 — y 1 = Δy или изменение по вертикали, а x 2 — x 1 = Δx или изменение по горизонтали, как показано на графике. Также можно видеть, что Δx и Δy являются отрезками, образующими прямоугольный треугольник с гипотенузой d , где d является расстоянием между точками и (х 2 , у 2 ) .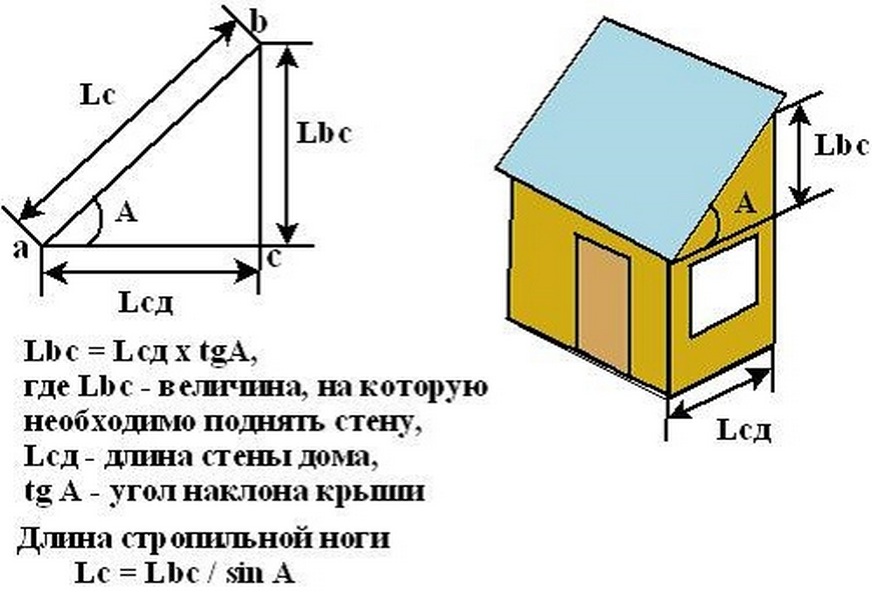 Поскольку Δx и Δy образуют прямоугольный треугольник, можно вычислить d по теореме Пифагора. Обратитесь к Калькулятору треугольника для получения более подробной информации о теореме Пифагора, а также о том, как рассчитать угол наклона θ , представленный в калькуляторе выше. Кратко:
Поскольку Δx и Δy образуют прямоугольный треугольник, можно вычислить d по теореме Пифагора. Обратитесь к Калькулятору треугольника для получения более подробной информации о теореме Пифагора, а также о том, как рассчитать угол наклона θ , представленный в калькуляторе выше. Кратко:
d = √(x 2 — x 1 ) 2 + (y 2 — y 1 ) 2
Вышеприведенное уравнение в корне является теоремой Пифагора, где гипотенуза d уже решена, а две другие стороны треугольника определяются вычитанием двух значений x и y , заданных двумя точками .Имея две точки, можно найти θ , используя следующее уравнение:
м = тангенс (θ)
Учитывая точки (3,4) и (6,8), найдите наклон линии, расстояние между двумя точками и угол наклона:
d = √(6 — 3) 2 + (8 — 4) 2 = 5
Хотя это выходит за рамки этого калькулятора, помимо его основного линейного использования, понятие наклона важно в дифференциальном исчислении. Для нелинейных функций скорость изменения кривой варьируется, а производная функции в данной точке — это скорость изменения функции, представленная наклоном линии, касательной к кривой в этой точке.
Для нелинейных функций скорость изменения кривой варьируется, а производная функции в данной точке — это скорость изменения функции, представленная наклоном линии, касательной к кривой в этой точке.
Расчет уклона и общих уклонов в архитектуре
Архитекторы постоянно предоставляют информацию об уклоне на своих чертежах, используя градиенты, градусы или проценты в зависимости от приложения. Например, крыши отмечаются с помощью уклонов, а поперечные уклоны тротуаров обычно обозначаются в градусах. Полезно понять, как рассчитать каждый метод.
Существует три различных способа указать наклон поверхности относительно горизонтальной плоскости: градусы, градиент и проценты.
Расчет градиента уклона
Градиенты уклона записываются как Y:X, где Y — единица подъема, а X — протяженность. Оба числа должны использовать одни и те же единицы измерения. Например, если вы путешествуете на 3 дюйма по вертикали и на 3 фута (36 дюймов) по горизонтали, уклон составит 3:36 или 1:12. Это читается как «один из двенадцати наклонов».
Это читается как «один из двенадцати наклонов».
Расчет процента уклона
Процент уклона рассчитывается почти так же, как градиент.Переведите рост и пробег в одни и те же единицы, а затем разделите рост на пробег. Умножьте это число на 100, и вы получите процент наклона. Например, подъем 3 дюйма, разделенный на длину 36 дюймов = 0,083 x 100 = уклон 8,3%.
Расчет уклона в градусах
Самый сложный способ расчета уклона — в градусах, и для этого требуется немного школьной математики. Тангенс данного угла (в градусах) равен подъему, деленному на пробег. Следовательно, арктангенс подъема, деленный на разбег, даст угол.
Таблица общих уклонов в архитектуре
В таблице ниже показаны некоторые распространенные наклоны. Полы с уклоном 1:20 не требуют поручней, но все, что круче 1:20, считается пандусом и требует наличия поручней. Пандусы с наклоном 1:12 — это максимальный уклон, разрешенный кодами ADA, и для них требуются поручни. Федеральные коды ADA указывают, что максимальный поперечный уклон доступного маршрута составляет 1:48, что составляет чуть более 2%. Однако мы видели некоторые юрисдикции, которые допускают максимальный поперечный уклон 1:50.
Федеральные коды ADA указывают, что максимальный поперечный уклон доступного маршрута составляет 1:48, что составляет чуть более 2%. Однако мы видели некоторые юрисдикции, которые допускают максимальный поперечный уклон 1:50.
| Степени | Градиентные | Процент | |||
|---|---|---|---|---|---|
| 0,6 ° | 1: 95.49 | 1,0% | |||
| 1 ° | 1: 57.29 | 1,7% | |||
| 1,15 ° | 1 : 50 | 2% | 2% | ||
| 1.19 ° 9 | 1: 48 | 2,08% | 2,08% | ||
| 2,86 ° 9 | 1: 20 | 5% | |||
| 4,76 ° 9 | 1: 12 | 8 .3% | |||
| 7.13 ° 9 | 7.13 ° 9 | 1: 8 | 12,5% | 12,5% | |
| 10 °30 | 1: 5.67 | 17,6% | 17,6% | ||
| 14.04 ° | 1: 4 | 25% | |||
| 15 ° | 1: 3. 73 73
| 1: 3.73 | 1: 3.73 | 26,8% | |
| 26.57 ° 2527 | 1: 2 | 50% | |||
| 1: 1.73 | 57.7% | ||||
| 45 ° | 1 : 1 | 100% | |||
| 56.31 ° | 1: 0.67 | 150% | |||
| 60 ° 30 | |||||
| 1: 0.6 | 1: 0.6 | 173,2% | 173,2% | ||
| 63.43 ° 2527 | 6%: 0.5 | 200% | |||
| 78.69 ° | 1 : 0.2 | 500327 | 500% | ||
| 89.43 ° 9 | 89.43 ° 9 | 1: 0,1 | 1000% | ||
| 90 ° | 1: 0 | INF. |
Уклоны крыши
Уклоны крыши идентифицируются с использованием описанного выше градиентного метода, где подъем варьируется, но длина ската обычно составляет 12.На некоторых очень крутых крышах вы можете увидеть перевернутый уклон, так что уклон меняется, но подъем сохраняется равным 12.
Крыши с малым уклоном
Крыши с малым уклоном имеют уклон 3:12 или меньше. Они должны иметь мембранную систему крыши для обеспечения водонепроницаемости.
| Градиент крыши | градусов | процентов | процент | |
|---|---|---|---|---|
| 1/4: 12 | 1/4: 12 | 1/19 ° | 2,08% | |
| 1/2: 12 | 2,39 ° | 4.17% | ||
| 1: 12 | 1: 12 | 4 | 4,76 °3 9047 9 | 9,3% |
| 2: 12 | 9.46 ° 6 | 16.67% | ||
| 3: 12 | 14.04 ° | 25% |
Крыши с крутым уклоном
Все, что выше 3:12, считается крутой крышей и может быть покрыто металлическими панелями, гонтом или черепицей — эти крыши не пропускают воду и не считаются водонепроницаемыми.
| Уклон крыши | Градусы | Проценты | ||
|---|---|---|---|---|
| 4 : 12 | 18. 43 ° 43 ° |
333% | ||
| 5: 12 | 5: 12 | 22.62 ° 9 | 9 22.62 ° | 41,67% | 6.57 ° 2527 | 50% |
| 7: 12 | 30.26 °3 | 58.33 % | ||
| : 12 | 33.69 ° 7 | 33,69 ° | 66.67% | 9: 12 |
| 9: 12 | 36.87 ° 2527 | 75% | ||
| 10: 12 | 39.81 ° 0 | 83,33% | ||
| 11 : 12 | 42.51° | 91,67% | ||
| 12 : 12 | 45° | 100% |
Как рассчитать уклон/градиент? «Восхождение над бегом» в науках о Земле
Многие из нас знают, что наклон линии рассчитывается как «подъем над пробегом». Однако применение расчета уклона может показаться несколько более сложным. В науках о земле вас могут попросить рассчитать уклон холма или определить скорость путем вычисления наклона линии на графике.Эта страница предназначена для того, чтобы помочь вам освоить эти навыки, чтобы вы могли использовать их в своих курсах по наукам о Земле.
Зачем мне вычислять наклон или градиент?
В геолого-геофизических исследованиях склон может играть важную роль в ряде задач. Наклон холма может помочь определить степень эрозии, вероятной во время ливня. Градиент уровня грунтовых вод может помочь нам понять, может ли (и в какой степени) загрязнение повлиять на местный колодец или источник воды.
Как рассчитать наклон (или градиент) в науках о Земле?
Градиент в случае склона холма и уровня грунтовых вод аналогичен расчету наклона линии на графике — «подъем» над «пробегом».Но как это сделать с помощью контурной (или топографической) карты?
- Сначала освойтесь с функциями интересующей вас топографической карты. Убедитесь, что вы знаете несколько вещей:
- Что такое контурный интервал (иногда сокращенно КИ)?
- Каков масштаб карты?
- Для какого элемента вы хотите узнать наклон?
Ниже представлена топографическая карта государственного парка Математика.
 Вы заинтересованы в построении пути от вершины холма на этой карте к ручью (Equation Creek) и хотите знать уклон холма. Возможно, вам следует распечатать карту (с инструкциями по расчету уклона) (Acrobat (PDF) 93kB Oct15 08).
Вы заинтересованы в построении пути от вершины холма на этой карте к ручью (Equation Creek) и хотите знать уклон холма. Возможно, вам следует распечатать карту (с инструкциями по расчету уклона) (Acrobat (PDF) 93kB Oct15 08).
.- Каков контурный интервал этой карты?
Интервал контура сообщает вам «подъем», в частности изменение высоты между каждой из «коричневых линий» (контуров). В этом случае контурный интервал находится в ключе справа внизу и обозначается аббревиатурой КИ. Интервал контура составляет 20 футов. - Каков масштаб карты?
Шкала показывает «пробег» или расстояние на земле.На этой карте он также показан в правом нижнем углу и показан только графически. Если вы распечатаете карту (с шагами для расчета уклона) (Acrobat (PDF) 93kB Oct15 08), вы обнаружите, что 1 дюйм = 1 миля. - Для какого объекта вы хотите узнать наклон?
В этом случае вам нужно узнать уклон склона холма к ЗСЗ от вершины (на высоте 869 футов) до ручья.
- Во-первых, вам нужно знать «подъем» для функции.«Подъем» — это разница высот сверху вниз (см. изображение выше). Так определите высоту вершины холма (или склона, или уровня грунтовых вод).
Вершина интересующего вас холма находится на высоте 859 футов. Горизонтальная линия у ручья, где заканчивается ваш путь, находится ниже 700 футов. Это составляет 680 футов (поскольку интервал контура равен 20 футам). Разница высот — это верх минус низ (859 футов — 680 футов), поэтому «подъем» = 179 футов
- Далее вам нужно знать «run» для функции.«Прогон» — это горизонтальное расстояние от самой высокой отметки до самой низкой. Итак, возьмите линейку и измерьте это расстояние. Зная масштаб, можно рассчитать расстояние. В большинстве случаев расстояние на картах указывается в км или милях.
Красная линия представляет собой расстояние вдоль склона холма, где вы хотите построить свой путь. Красная линия в два раза длиннее шкалы одной мили (на печатной карте она составляет около 2 дюймов).
 Таким образом, расстояние от вершины холма до подножия или «пробег» = 2 мили
Таким образом, расстояние от вершины холма до подножия или «пробег» = 2 мили - Теперь идет подъем над беговой частью.Есть два способа, которыми вас могут попросить сделать расчеты, относящиеся к уклону. Убедитесь, что вы знаете, о чем вас спрашивают, и выполните шаги, связанные с соответствующим процессом:
- Если вас попросят рассчитать уклон (как в линии или на склоне холма), достаточно простого деления. Просто убедитесь, что вы следите за единицами!
- Как мы уже видели на этой странице, наклон «возвышается над уступом». Фраза «подниматься над бегом» подразумевает, что вам нужно будет разделиться.Уравнение для наклона выглядит следующим образом:
- Возьмите разницу высот и разделите ее на разницу по горизонтали (всегда следите за единицами измерения).
На карте Math State Park высота холма = 179 футов, а длина пробега — 2 мили. Итак, мы ставим задачу следующим образом: - Завершите расчет с помощью калькулятора (или выполните расчеты вручную).

Теперь просто делим подъем на разбег и получаем:Единицами, которые вы получите, могут быть футы/мили, м/км или футы/футы (уклон может быть выражен всеми этими способами).Это просто зависит от того, с чего вы начали.
- Вас также могут попросить вычислить процент (или %) уклона . Этот расчет занимает пару шагов. И это в основном связано с уделением внимания единицам. Единицы как на подъеме, так и на бегу должны быть одинаковыми.
- Для расчета уклона в процентах значения подъема и прогона должны быть равны в одних и тех же единицах измерения (например, в футах или метрах).Если ваше горизонтальное расстояние указано в милях, вам нужно преобразовать его в футы; если горизонтальное расстояние указано в километрах, вам придется преобразовать его в метры. (Чтобы преобразовать мили в футы, умножьте на 5280 футов/милю; км в м умножьте на 1000 м/км.
 Если вам нужна дополнительная помощь с этим или нужно преобразовать другие единицы, см. модуль преобразования единиц измерения).
Если вам нужна дополнительная помощь с этим или нужно преобразовать другие единицы, см. модуль преобразования единиц измерения).
Прямо сейчас у вас рост в футах и пробег в милях. Давайте переведем мили в футы, умножив их на соответствующий коэффициент преобразования: 1 миля = 5280 футов.Итак, мы должны умножить «бег» на: - После того, как вы преобразовали так, чтобы и высота, и расстояние имели одинаковые единицы измерения, мы можем написать уравнение для уклона: подъем над пробегом (подразумевается, что высота разделена на пробег).
Мы знаем, что подъем составляет 179 футов, а пробег — 10560 футов:
Но подождите, есть еще один шаг, чтобы добраться до % наклона. - Чтобы получить %, нам нужно умножить рассчитанный наклон (который не имеет единиц измерения, поскольку единицы измерения сокращаются вверху и внизу) на 100, чтобы наше уравнение выглядело следующим образом:
Начните с подъема над разбегом и умножьте на 100:
- Теперь подставьте свои числа и рассчитайте % наклона!
Обратите внимание, что % уклона не имеет единиц измерения, потому что ft отменяется при расчете.
 Однако убедитесь, что вы указали, что это %!
Однако убедитесь, что вы указали, что это %! - Я ГОТОВ практиковаться (ответы на эти задачи сработали)
Следующие шаги
Калькулятор уклона
Использование калькулятора
Наклон линии — это ее вертикальное изменение, деленное на ее горизонтальное изменение, также известное как превышение над бегом.Когда у вас есть 2 точки на линии на графике, наклон представляет собой изменение y, деленное на изменение x.
Наклон линии — это мера ее крутизны.
Решения для расчета уклона
Введите две точки, используя числа, дроби, смешанные числа или десятичные дроби. Калькулятор уклона показывает работу и дает следующие решения уклона:
- Уклон м с двумя точками
- График линии для y = mx + b
- Форма уклона точки y — y 1 = m(x — x 1 )
- Форма пересечения наклона y = mx + b
- Стандартная форма Ax + By = C
- y-отрезок, когда x = 0
- x-пересечение, когда y = 0
Вам также будет предоставлена настраиваемая ссылка на
Калькулятор средней точки, который решит и покажет работу, чтобы найти среднюю точку и расстояние для заданных двух точек.
Как рассчитать наклон линии
Расчет уклона, м по формуле для уклона:
Формула уклона
\[ m = \dfrac {(y_{2} — y_{1})} {(x_{2} — x_{1})} \] \[ m = \dfrac{rise}{run} = \dfrac{ \Delta y}{\Delta x} = \dfrac{y_2 — y_1}{x_2 — x_1} \]
Здесь вам нужно знать координаты 2 точек на прямой, (x 1 , y 1 ) и (x 2 , y 2 ).
Как найти наклон линии
- Найдите разницу между координатами y, Δy — изменение y
- Найдите разницу между координатами x, Δx — это изменение x
- Разделите Δy на Δx, чтобы найти уклон
Δу = у 2 — у 1
Δх = х 2 — х 1
м = Δy/Δx
Пример: найти уклон
Допустим, вы знаете две точки на прямой и их координаты (2, 5) и (9, 19). Найдите наклон, найдя разницу в точках y, и разделите ее на разницу в точках x.
Найдите наклон, найдя разницу в точках y, и разделите ее на разницу в точках x.
- Разница между координатами y Δy составляет
- Разница между координатами x Δx равна
- Разделите Δy на Δx, чтобы найти уклон м
Δу = у 2 — у 1
Δy = 19 — 5
Δy = 14
Δх = х 2 — х 1
Δx = 9 — 2
Δx = 7
\( м = \dfrac {14} {2} \)
\(м = 7 \)
Уравнения линий с наклоном
Существует 3 распространенных способа записи линейных уравнений с наклоном:
- Точечный откос
- Форма пересечения уклона
- Типовая форма
Точечная форма уклона записывается как
у — у 1 = м (х — х 1 )
Используя координаты одной из точек на линии, вставьте значения в точки x1 и y1, чтобы получить уравнение линии в форме точечного наклона.
Давайте используем точку из исходного примера выше (2, 5) и наклон, который мы рассчитали как 7. Поместите эти значения в формат наклона точки, чтобы получить уравнение этой линии в форме наклона точки:
у — 5 = 7(х — 2)
Если вы упростите приведенное выше уравнение наклона точки, вы получите уравнение линии в форме пересечения наклона.
Форма пересечения наклона записывается как
у = м х + б
Возьмите уравнение формы наклона точки и умножьте 7 на х и 7 на 2.
у — 5 = 7(х — 2)
у — 5 = 7х — 14
Продолжайте работать над уравнением так, чтобы у было по одну сторону от знака равенства, а все остальное по другую сторону.
Добавьте 5 к обеим частям уравнения, чтобы получить уравнение в форме пересечения наклона:
у = 7х — 9
Стандартная форма уравнения для линии записывается как
Топор + В = С
В некоторых ссылках вы также можете встретить стандартную форму, записанную как Ax + By + C = 0.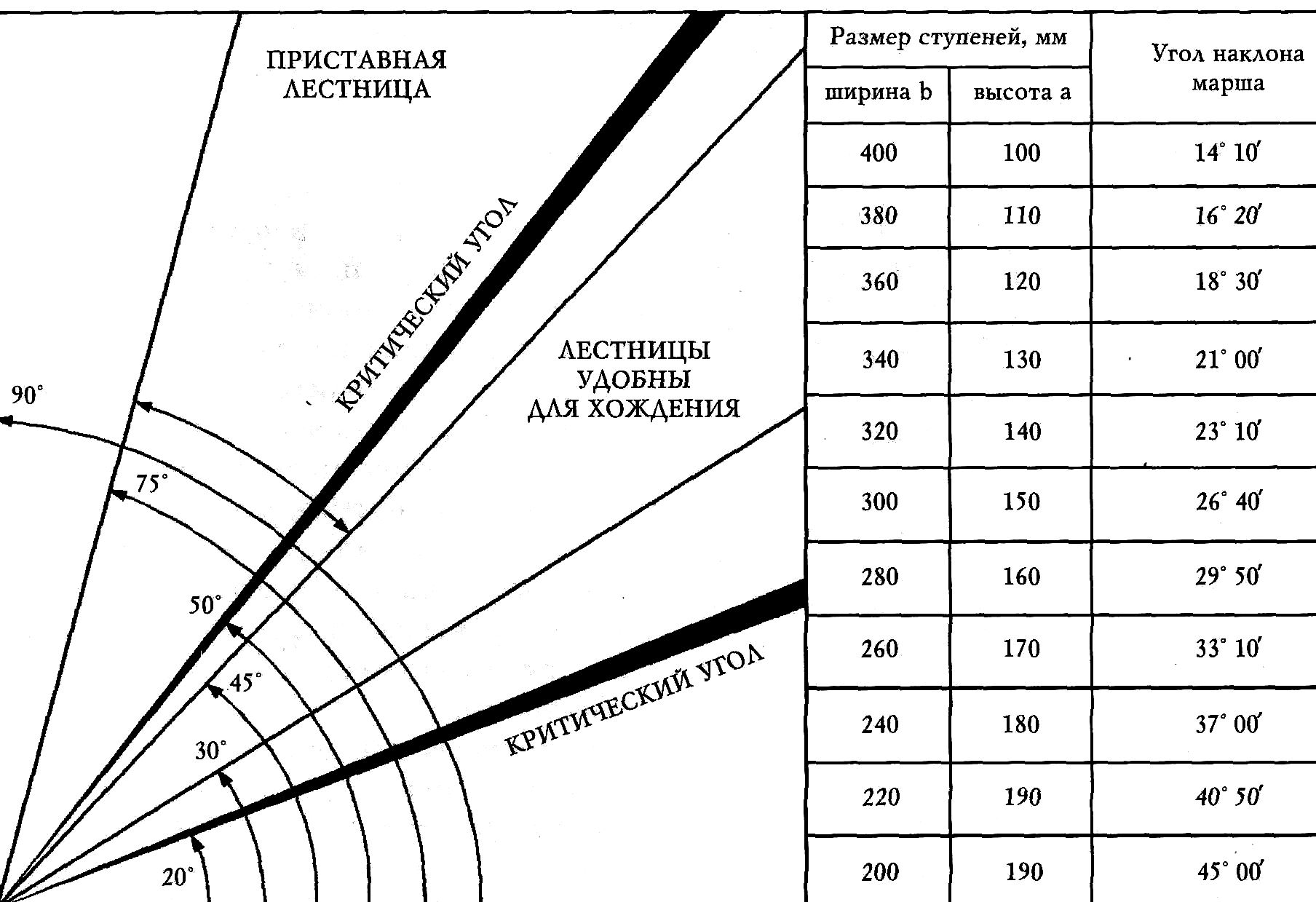
Используйте либо формулу формы точки наклона, либо формулу пересечения наклона и выполните математические вычисления, чтобы преобразовать уравнение в стандартную форму. Обратите внимание, что уравнение не должно включать дроби или десятичные знаки, а коэффициент x должен быть только положительным.
Форма пересечения наклона: y = 7x — 9
Вычтите y из обеих частей уравнения, чтобы получить 7x — y — 9 = 0
Добавьте 9 к обеим частям уравнения, чтобы получить 7x — y = 9
Форма пересечения наклона y = 7x — 9 становится 7x — y = 9, записанной в стандартной форме.
Найти наклон по уравнению
Если у вас есть уравнение для прямой, вы можете представить его в форме пересечения наклона. Коэффициент x будет наклоном.
Пример
У вас есть уравнение прямой, 6x — 2y = 12, и вам нужно найти наклон.
Ваша цель — преобразовать уравнение в формат пересечения наклона y = mx + b
- Начните с вашего уравнения 6x — 2y = 12
- Добавьте 2y к обеим сторонам, чтобы получить 6x = 12 + 2y
- Вычтите 12 из обеих частей уравнения, чтобы получить 6x — 12 = 2y
- Вы хотите получить y в одной части уравнения, поэтому вам нужно разделить обе части на 2, чтобы получить y = 3x — 6
- Это форма пересечения наклона, y = 3x — 6.Наклон — это коэффициент x, поэтому в этом случае наклон = 3
.
Как найти точку пересечения оси Y
Точка пересечения линии по оси y представляет собой значение y, когда x=0. Это точка пересечения прямой с осью Y.
Используя уравнение y = 3x — 6, установите x=0, чтобы найти точку пересечения с осью y.
у = 3(0) — 6
г = -6
Y-пересечение равно -6
Как найти x-Intercept
Пересечение линии по оси x равно значению x при y=0. Это точка пересечения прямой с осью x.
Это точка пересечения прямой с осью x.
Используя уравнение y = 3x — 6, установите y=0, чтобы найти точку пересечения по оси x.
0 = 3x — 6
3x = 6
х = 2
X-пересечение равно 2
Наклон параллельных линий
Если известен наклон линии, любая параллельная ей линия будет иметь такой же наклон, и эти линии никогда не пересекутся.
Наклон перпендикулярных линий
Если известен наклон линии, любая линия, перпендикулярная к ней, будет иметь наклон, равный отрицательной обратной величине известного наклона.
Перпендикуляр означает, что линии образуют угол 90° при пересечении.
Допустим, у вас есть линия с наклоном -4. Каков наклон прямой, перпендикулярной к ней?
- Сначала возьмите отрицательный наклон вашей линии
-(-4) = 4 - Во-вторых, возьмите обратное число.
 4 — целое число, поэтому его знаменатель равен 1. Обратное 4/1 равно 1/4.
4 — целое число, поэтому его знаменатель равен 1. Обратное 4/1 равно 1/4. - Отрицательная инверсия наклона -4 равна наклону 1/4.
- Линия, перпендикулярная исходной линии, имеет наклон 1/4.
Дальнейшее изучение
Брайан Маклоган (2014) Определение наклона между двумя точками в виде дробей, 10 июня. На https://www.youtube.com/watch?v=Hz_eapwVcrM
Определение наклона линии
Ранее в уроке 3 мы узнали, что наклон линии на графике зависимости положения от времени равен скорости объекта.Если объект движется со скоростью +4 м/с, то наклон линии будет +4 м/с. Если объект движется со скоростью -8 м/с, то наклон линии будет -8 м/с. Если объект имеет скорость 0 м/с, то наклон линии будет 0 м/с. Наклон линии на графике зависимости позиции от времени говорит сам за себя. Из-за его важности изучающий физику должен хорошо понимать, как вычислить наклон линии. В этой части урока будет обсуждаться метод определения наклона линии на позиционно-временном графике.
В этой части урока будет обсуждаться метод определения наклона линии на позиционно-временном графике.
Давайте начнем с рассмотрения приведенного ниже графика зависимости позиции от времени.
Линия имеет наклон вверх вправо. Но математически, насколько он наклоняется вверх за каждую 1 секунду по горизонтальной (временной) оси? Чтобы ответить на этот вопрос, мы должны использовать уравнение наклона.
Использование уравнения наклона
Уравнение наклона говорит о том, что наклон линии находится путем определения величины подъема линии между любыми двумя точками, деленной на величину пробега линии между теми же двумя точками.Другими словами,
- Выберите две точки на линии и определите их координаты.
- Определить разницу координат y этих двух точек ( рост ).
- Определить разницу координат x для этих двух точек ( запустить ).
- Разделить разницу в координатах y на разницу в координатах x (подъем/спуск или уклон).

На приведенной ниже диаграмме показано применение этого метода для определения наклона линии.Обратите внимание, что три разных вычисления выполняются для трех разных наборов из двух точек на линии. В каждом случае результат один и тот же: уклон равен 10 м/с.
Так что это было просто — подъем над бегом — это все, что нужно.
Теперь рассмотрим более сложный пример. Рассмотрим график ниже. Обратите внимание, что наклон не положительный, а скорее отрицательный; то есть линия наклонена в нисходящем направлении. Заметим также, что линия на графике не проходит через начало координат.Расчет уклона относительно прост, когда линия проходит через начало координат, поскольку одна из точек равна (0,0). Но это не тот случай. Проверьте свое понимание расчета уклона, определив наклон приведенной ниже линии. Затем нажмите кнопку, чтобы проверить свой ответ.
Проверьте свое понимание
1. Определите скорость (т. е. наклон) объекта, как показано на графике ниже.Когда вы поверите, что знаете ответ (и не раньше), нажмите кнопку, чтобы проверить его.
Определите скорость (т. е. наклон) объекта, как показано на графике ниже.Когда вы поверите, что знаете ответ (и не раньше), нажмите кнопку, чтобы проверить его.
графических навыков: четвертый блок
графических навыков: четвертый блок
Расчет уклона
Чтобы вычислить наклон линии, вам нужно всего две точки из
эта строка, ( x 1, y 1) и ( x 2, y 2).
| Уравнение, используемое для расчета наклона по двум точкам: | На графике это можно представить как: |
Существует три этапа вычисления наклона прямой.
линия, когда вам не дано ее уравнение.
- Шаг первый:
Определите две точки на прямой.
- Шаг второй:
Выберите один из них ( x 1, y 1)
а другой должен быть ( x 2, y 2). - Шаг третий:
Используйте уравнение наклона для расчета уклона.
Найдите минутку, чтобы проработать пример, в котором нам дается
две точки.
Пример
Допустим, точки (15, 8) и (10, 7) лежат на прямой.
Каков наклон этой линии?
- Шаг первый:
Определите две точки на прямой.В этом примере нам даны две точки, (15, 8) и (10, 7),
по прямой. - Шаг второй:
Выберите один из них ( x 1, y 1)
а другой должен быть ( x 2, y 2).Неважно, что мы выберем, так что пусть (15, 8) будет
( х 2, у 2). Возьмем точку (10,
7) быть точкой ( х 1,
и 1). - Шаг третий:
Используйте уравнение для расчета уклона.После того, как мы завершили шаг 2, мы готовы вычислить наклон
используя уравнение для наклона:Мы сказали, что на самом деле не имеет значения, какую точку мы выберем
как ( x 1, y 1) и каким быть ( x 2, y 2).
Покажем, что это правда. Возьмите те же две точки (15, 8)
и (10, 7), но на этот раз мы будем вычислять наклон, используя (15,
8) как ( x 1, y 1) и (10, 7) как точка ( x 2, y 2).Затем подставьте их в уравнение для наклона:Получаем тот же ответ, что и раньше!
Часто вам не дадут два балла, но вам нужно будет
определить две точки на графике. В этом случае процесс
то же самое, первым шагом является определение точек из
график. Ниже приведен пример, который начинается с графика.
Пример
|
Каков наклон линии, изображенной на графике? Наклон этой линии равен 2. |
[подробное решение к примеру]
Теперь найдите минутку и сравните две линии на
тот же график.
|
Обратите внимание, что линия с большим наклоном является более крутой из |
Теперь вы готовы решить практическую задачу. Если вы уже
выполнили первую практическую задачу для этого модуля, который вы можете пожелать
попробовать дополнительную практику.
.


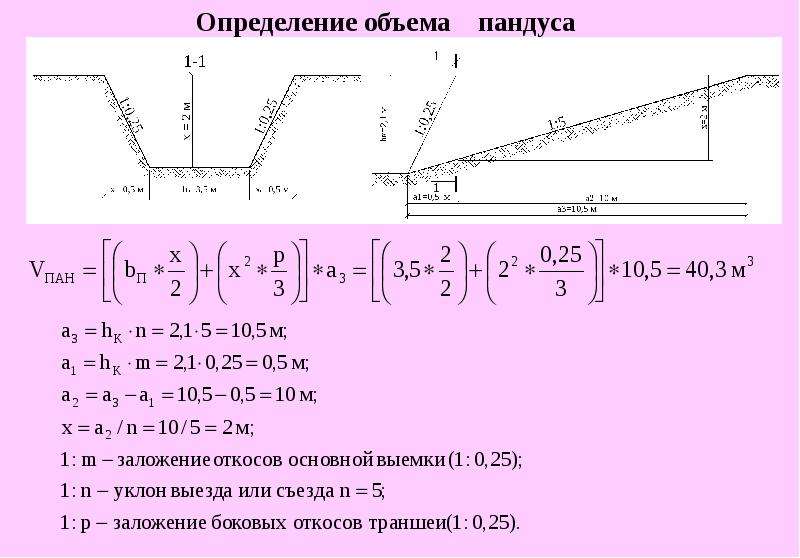
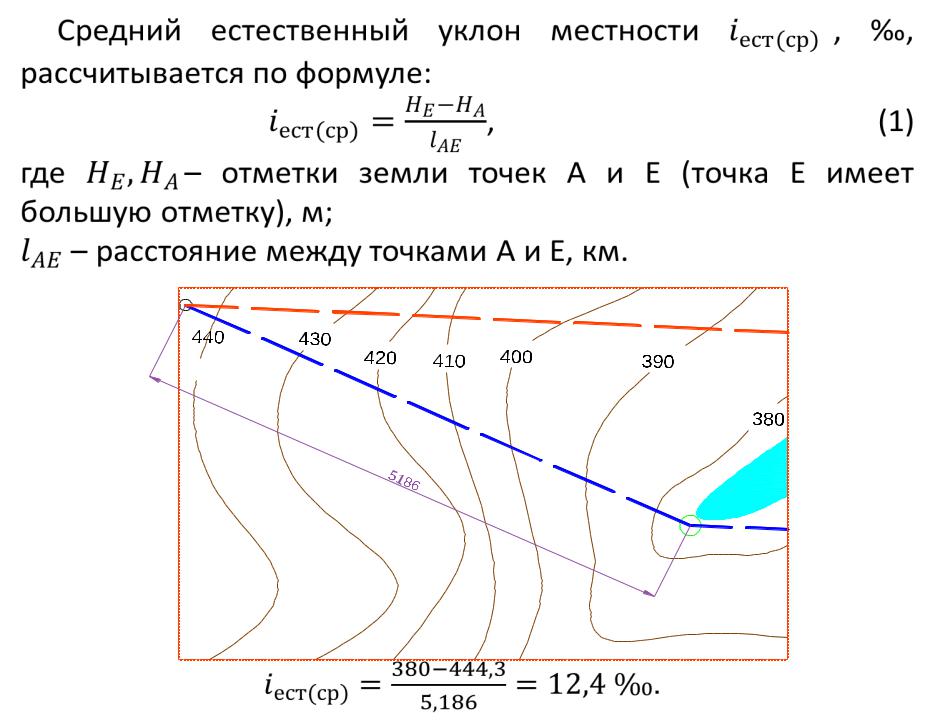 Из размера наибольшей высоты клина вычтем размер наименьшей высоты: 50 – 40 = 10 мм. Разность между этими величинами можно рассматривать как размер катета прямоугольного треугольника, образовавшегося после проведения на чертеже горизонтальной линии (рис. 6.40, б). Величиной уклона будет отношение размера меньшего катета к размеру горизонтальной линии. В данном случае нужно разделить 10 на 100. Величина уклона клина будет 1:10.
Из размера наибольшей высоты клина вычтем размер наименьшей высоты: 50 – 40 = 10 мм. Разность между этими величинами можно рассматривать как размер катета прямоугольного треугольника, образовавшегося после проведения на чертеже горизонтальной линии (рис. 6.40, б). Величиной уклона будет отношение размера меньшего катета к размеру горизонтальной линии. В данном случае нужно разделить 10 на 100. Величина уклона клина будет 1:10. Например, чтобы провести линию, уклон которой 1:4, через концевую точку вертикальной линии (рис. 6.42), отрезок прямой линии длиной 10 мм следует принять за единицу длины и отложить на продолжении горизонтальной линии четыре такие единицы (т.е. 40 мм). Затем через крайнее деление и верхнюю точку отрезка провести прямую линию.
Например, чтобы провести линию, уклон которой 1:4, через концевую точку вертикальной линии (рис. 6.42), отрезок прямой линии длиной 10 мм следует принять за единицу длины и отложить на продолжении горизонтальной линии четыре такие единицы (т.е. 40 мм). Затем через крайнее деление и верхнюю точку отрезка провести прямую линию. Рассматриваемая фигура образуется телом вращения, которому свойственен диаметральный показатель. В случае конуса их может быть несколько, а изменение показателя происходит плавно, не ступенчато. Как правило, у подобной фигуры есть больший диаметр, а также промежуточной в случае наличия ступени.
Рассматриваемая фигура образуется телом вращения, которому свойственен диаметральный показатель. В случае конуса их может быть несколько, а изменение показателя происходит плавно, не ступенчато. Как правило, у подобной фигуры есть больший диаметр, а также промежуточной в случае наличия ступени.
 Для правильного отображения используется табличная информация.
Для правильного отображения используется табличная информация. В большинстве случаев обработка проводится именно при учете угла, а не показателей большого и малого диаметра.
В большинстве случаев обработка проводится именно при учете угла, а не показателей большого и малого диаметра. ru/instrumenty/formula-rascheta-ugla-konusa
ru/instrumenty/formula-rascheta-ugla-konusa Длину одного из катетов принимают равной 100 %, а другого — 20 %.
Длину одного из катетов принимают равной 100 %, а другого — 20 %. 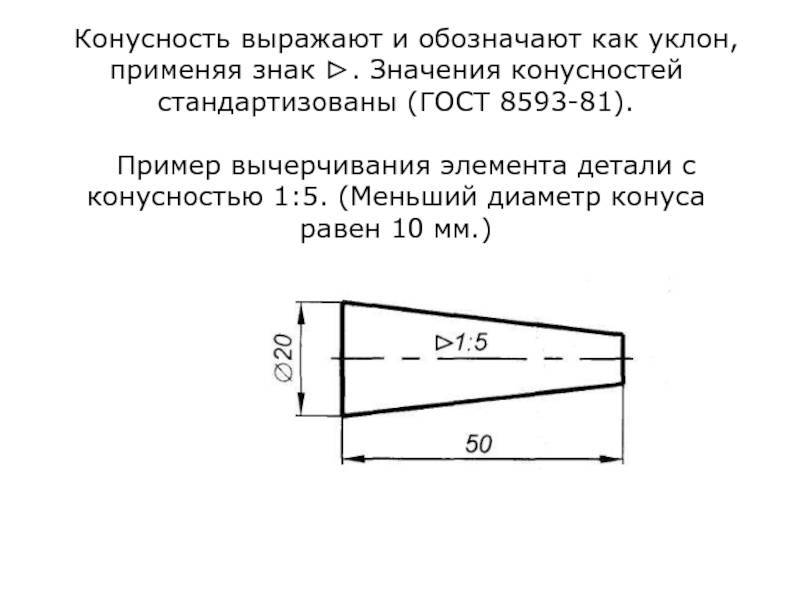

 Кроме этого, были разработаны самые различные таблицы соответствия, которые могут применяться при проведении непосредственных расчетов.
Кроме этого, были разработаны самые различные таблицы соответствия, которые могут применяться при проведении непосредственных расчетов. Это связано с трудностями, которые возникают на производственной линии.
Это связано с трудностями, которые возникают на производственной линии.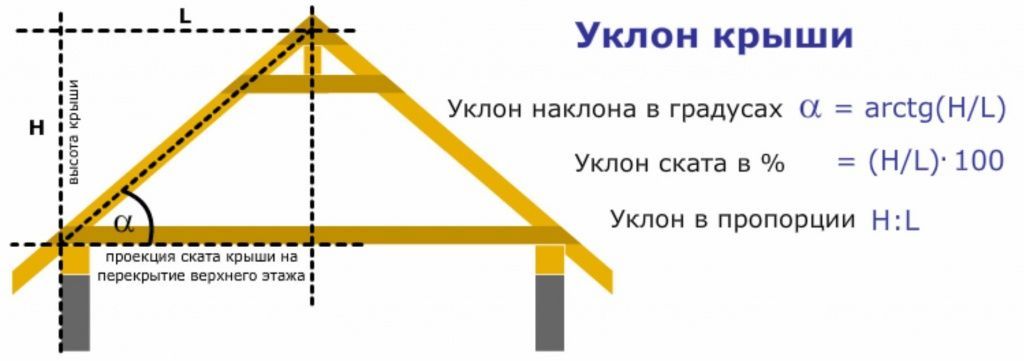 ru/blog/1719-postroenie-uklona-i-konusnosti.html: использовано 1 блоков из 3, кол-во символов 1374 (12%)
ru/blog/1719-postroenie-uklona-i-konusnosti.html: использовано 1 блоков из 3, кол-во символов 1374 (12%) Чем круче кровля, тем сильнее ее парусная способность. Поэтому в регионах с сильным, порывистым ветром предпочтительнее более пологие кровельные конструкции. Хотя с другой стороны, с низкоуклонных скатов ветром может срывать гидроизоляционный материал.
Чем круче кровля, тем сильнее ее парусная способность. Поэтому в регионах с сильным, порывистым ветром предпочтительнее более пологие кровельные конструкции. Хотя с другой стороны, с низкоуклонных скатов ветром может срывать гидроизоляционный материал. Вы заинтересованы в построении пути от вершины холма на этой карте к ручью (Equation Creek) и хотите знать уклон холма. Возможно, вам следует распечатать карту (с инструкциями по расчету уклона) (Acrobat (PDF) 93kB Oct15 08).
Вы заинтересованы в построении пути от вершины холма на этой карте к ручью (Equation Creek) и хотите знать уклон холма. Возможно, вам следует распечатать карту (с инструкциями по расчету уклона) (Acrobat (PDF) 93kB Oct15 08).
 Таким образом, расстояние от вершины холма до подножия или «пробег» = 2 мили
Таким образом, расстояние от вершины холма до подножия или «пробег» = 2 мили 
 Если вам нужна дополнительная помощь с этим или нужно преобразовать другие единицы, см. модуль преобразования единиц измерения).
Если вам нужна дополнительная помощь с этим или нужно преобразовать другие единицы, см. модуль преобразования единиц измерения). Однако убедитесь, что вы указали, что это %!
Однако убедитесь, что вы указали, что это %! 4 — целое число, поэтому его знаменатель равен 1. Обратное 4/1 равно 1/4.
4 — целое число, поэтому его знаменатель равен 1. Обратное 4/1 равно 1/4. 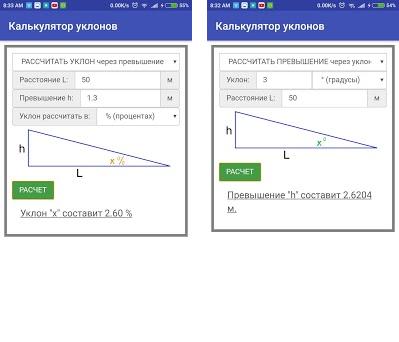


 Чем больше наклон, тем круче линия. Держите в
Чем больше наклон, тем круче линия. Держите в