Объем жидкости в трубе: ОБЪЕМ ВОДЫ В ТРУБАХ
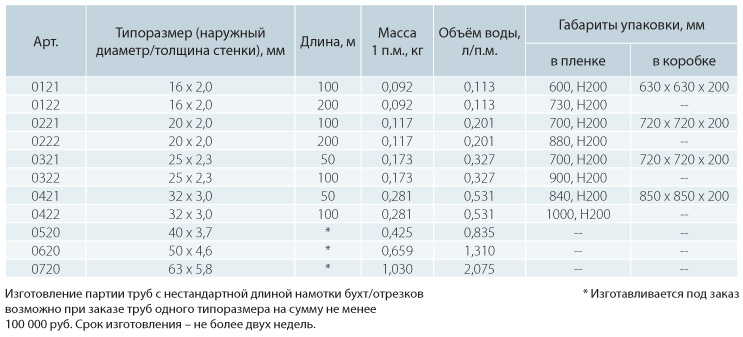
ОБЪЕМ ВОДЫ В ТРУБАХ
ОБЪЕМ ВОДЫ В ТРУБАХ
| Внутренний диаметр трубы, мм | Внутренний объем 1м погонного трубы, литров | Внутренний объем 10 м погонных трубы, литров |
|---|---|---|
| 4 | 0,0126 | 0,1257 |
| 5 | 0,0196 | 0,1963 |
| 6 | 0,0283 | 0,2827 |
| 7 | 0,0385 | 0,3848 |
| 8 | 0,0503 | 0,5027 |
| 9 | 0,0636 | 0,6362 |
| 10 | 0,0785 | 0,7854 |
| 11 | 0,0950 | 0,9503 |
| 12 | 0,1131 | 1,1310 |
| 13 | 0,1327 | 1,3273 |
| 14 | 0,1539 | 1,5394 |
| 15 | 0,1767 | 1,7671 |
| 16 | 0,2011 | 2,0106 |
| 17 | 0,2270 | 2,2698 |
| 18 | 0,2545 | 2,5447 |
| 19 | 0,2835 | 2,8353 |
| 20 | 0,3142 | 3,1416 |
| 21 | 0,3464 | 3,4636 |
| 22 | 0,3801 | 3,8013 |
| 23 | 0,4155 | 4,1548 |
| 24 | 0,4524 | 4,5239 |
| 26 | 0,5309 | 5,3093 |
| 28 | 0,6158 | 6,1575 |
| 30 | 0,7069 | 7,0686 |
| 32 | 0,8042 | 8,0425 |
| 34 | 0,9079 | 9,0792 |
| 36 | 1,0179 | 10,1788 |
| 38 | 1,1341 | 11,3411 |
| 40 | 1,2566 | 12,5664 |
| 42 | 1,3854 | 13,8544 |
| 44 | 1,5205 | 15,2053 |
| 46 | 1,6619 | 16,6190 |
| 48 | 1,8096 | 18,0956 |
| 50 | 1,9635 | 19,6350 |
| 52 | 2,1237 | 21,2372 |
| 54 | 2,2902 | 22,9022 |
| 56 | 2,4630 | 24,6301 |
| 58 | 2,6421 | 26,4208 |
| 60 | 2,8274 | 28,2743 |
| 62 | 3,0191 | 30,1907 |
| 64 | 3,2170 | 32,1699 |
| 66 | 3,4212 | 34,2119 |
| 68 | 3,6317 | 36,3168 |
| 70 | 3,8485 | 38,4845 |
| 72 | 4,0715 | 40,7150 |
| 74 | 4,3008 | 43,0084 |
| 76 | 4,5365 | 45,3646 |
| 78 | 4,7784 | 47,7836 |
| 82 | 5,2810 | 52,8102 |
| 84 | 5,5418 | 55,4177 |
| 86 | 5,8088 | 58,0880 |
| 88 | 6,0821 | 60,8212 |
| 90 | 6,3617 | 63,6173 |
| 92 | 6,6476 | 66,4761 |
| 94 | 6,9398 | 69,3978 |
| 96 | 7,2382 | 72,3823 |
| 98 | 7,5430 | 75,4296 |
| 100 | 7,8540 | 78,5398 |
| 105 | 8,6590 | 86,5901 |
| 110 | 9,5033 | 95,0332 |
| 115 | 10,3869 | 103,8689 |
| 120 | 11,3097 | 113,0973 |
| 125 | 12,2718 | 122,7185 |
| 130 | 13,2732 | 132,7323 |
| 135 | 14,3139 | 143,1388 |
| 140 | 15,3938 | 153,9380 |
| 145 | 16,5130 | 165,1300 |
| 150 | 17,6715 | 176,7146 |
| 160 | 20,1062 | 201,0619 |
| 170 | 22,6980 | 226,9801 |
| 180 | 25,4469 | 254,4690 |
| 190 | 28,3529 | 283,5287 |
| 200 | 31,4159 | 314,1593 |
| 210 | 34,6361 | 346,3606 |
| 220 | 38,0133 | 380,1327 |
| 230 | 41,5476 | 415,4756 |
| 240 | 45,2389 | 452,3893 |
| 250 | 49,0874 | 490,8739 |
| 260 | 53,0929 | 530,9292 |
| 270 | 57,2555 | 572,5553 |
| 280 | 61,5752 | 615,7522 |
| 290 | 66,0520 | 660,5199 |
| 300 | 70,6858 | 706,8583 |
| 320 | 80,4248 | 804,2477 |
| 340 | 90,7920 | 907,9203 |
| 360 | 101,7876 | 1017,8760 |
| 380 | 113,4115 | 1134,1149 |
| 400 | 125,6637 | 1256,6371 |
| 420 | 138,5442 | 1385,4424 |
| 440 | 152,0531 | 1520,5308 |
| 460 | 166,1903 | 1661,9025 |
| 480 | 180,9557 | 1809,5574 |
| 500 | 196,3495 | 1963,4954 |
| 520 | 212,3717 | 2123,7166 |
| 540 | 229,0221 | 2290,2210 |
| 560 | 246,3009 | 2463,0086 |
| 580 | 264,2079 | 2642,0794 |
| 600 | 282,7433 | 2827,4334 |
| 620 | 301,9071 | 3019,0705 |
| 640 | 321,6991 | 3216,9909 |
| 660 | 342,1194 | 3421,1944 |
| 680 | 363,1681 | 3631,6811 |
| 700 | 384,8451 | 3848,4510 |
| 720 | 407,1504 | 4071,5041 |
| 740 | 430,0840 | 4300,8403 |
| 760 | 453,6460 | 4536,4598 |
| 780 | 477,8362 | 4778,3624 |
| 800 | 502,6548 | 5026,5482 |
| 820 | 528,1017 | 5281,0173 |
| 840 | 554,1769 | 5541,7694 |
| 860 | 580,8805 | 5808,8048 |
| 880 | 608,2123 | 6082,1234 |
| 900 | 636,1725 | 6361,7251 |
| 920 | 664,7610 | 6647,6101 |
| 940 | 693,9778 | 6939,7782 |
| 960 | 723,8229 | 7238,2295 |
| 980 | 754,2994 | 7542,9640 |
| 1000 | 785,3982 | 7853,9816 |
Обратная связь
Обратная связь
|
Внутренний диаметр трубы 4-1000 мм. Масса воды в трубе. Сколько нужно воды или антифриза или теплоносителя или, там, вазелина;) … для наполнения
1 м трубы,
1 м трубы,Как рассчитать объём воды в трубах
Сколько воды расходуется по статье «общедомовые нужды»
при сбросе стояков?
Как выбрать гидроаккумулятор?
Сколько антифриза покупать для заполнения системы отопления коттеджа?
ПАМЯТКА
как рассчитать объем воды в трубе
Объем воды в трубах вычисляется как сумма произведений объемов воды в метре трубы каждого диаметра на количество метров труб данного диаметра.
Объем гидроаккумулятора для системы отопления должен составлять 10-12 % объема всей воды в системе. Последняя цифра складывается из объема воды во всех радиаторах отопления, плюс объема воды в котле отопления, плюс объем воды в трубах для отопления.
Объем воды в радиаторах складывается из объема воды в каждой секции радиатора, помноженном на количество секций. Это значение указывается в технических паспортах на радиаторы. Смотрим технический паспорт.
Объем воды в котле отопления указывается в паспорте. Этот объем полезно знать также при спуске воды из отдельных частей системы отопления.
Таблица объема воды
в неармированных и армированных алюминием полипропиленовых трубах:
|
Номинальный размер (внешний диаметр), мм
|
Внутреннее сечение, мм кв.
|
Объем воды в метре трубы, литры
|
Внутренний диаметр, мм
|
Соответствующий им диаметр стальных дюймовых труб, дюймы
|
|
20
|
136,7
|
0,137
|
13,2
|
1/2
|
|
25
|
216,3
|
0,216
|
16,6
|
3/4
|
|
32
|
352,8
|
0,353
|
21,2
|
1
|
|
40
|
555,4
|
0,555
|
26,6
|
1 1/4 (дюйм с четвертью)
|
|
50
|
865,3
|
0,865
|
33,2
|
1 1/2
|
|
63
|
1384,7
|
1,385
|
42
|
2
|
|
75
|
1962,5
|
1,963
|
50
|
2 1/2
|
|
90
|
2826
|
2,826
|
60
|
3
|
|
110
|
4206,2
|
4,206
|
73,2
|
|
Таблица объема воды в стальных трубах:
|
Номинальный размер, дюймы
|
Внешний диаметр, мм
|
Внутренний диаметр, мм
|
Внутреннее сечение, мм
|
Объем воды в метре трубы, литры
|
|
1/4
|
13,5
|
9,5
|
29,83
|
0,03 (30 миллилитров)
|
|
3/8
|
17
|
13
|
133
|
0,133
|
|
1/2 (полдюйма)
|
21,3
|
16,3
|
209
|
0,209
|
|
3/4
|
26,8
|
21,8
|
373
|
0,373
|
|
1
|
33,5
|
27,9
|
611
|
0,611
|
|
1 1/4 (дюйм с четвертью)
|
42,3
|
36,7
|
1057
|
1,057
|
|
1 1/2
|
48
|
42
|
1385
|
1,385
|
|
2
|
60
|
54
|
2289
|
2,289
|
Объем воды в стальных трубах больше количества воды в соответствующих пластиковых трубах Внутренняя поверхность пластиковых труб гладкая, а стальных труб шероховатая.
В результате пластиковые трубы (как и медные) меньшего диаметра пропускают столько же воды, сколько и стальные трубы, имеющие больший внутренний диаметр.
Генеральный директор
ООО «ОСТРОУМОВ» Д.Ю. Остроумов
Объем воды в трубе | Мир инженера
В этой статье, я Вам расскажу, как правильно рассчитывать объем воды в трубе и массу воды. Очень часто во время проектированию приходится подбирать водоприемные колодцы для удаления воды из трубопроводов, так называемые спускники. За свою проектную практику встречал много разных специалистов инженеров-проектировщиков с большим стажем, которые сидят на высоких должностях в проектных организациях, а объем воды в трубах подсчитать не могут. Так что, надо им показать, как все же считать, а то работают и не краснеют. Есть такие даже инженеры, которые до сих пор задают такие вопросы — 1 миллилитр сколько литров, сколько литров в кубическом метре? Ответы будут ниже в статье.
Итак приступим. Как все же рассчитать объем воды в трубе? Труба – это обычный длинный цилиндр. Так что, объем цилиндра нас считать учили еще в школе, на уроках – математики, геометрии, физики. Так что я не понимаю, чего сложного в этом расчете!
Объем цилиндра равен: V = Пи*R*R*H
Пи – число Пи=3,14
R – радиус цилиндра в метрах ( если диаметр трубы Ду100 мм, то R=0,05 м)
Н – высота цилиндра, другими словами длина трубы.
Я все объемы уже подсчитал на 1 метр трубы, и когда мне нужно рассчитать объем воды в трубе определенной длины, я всего лишь умножаю объем 1 п.м. на метраж трубы.
Так же для тех, кто предпочитает справочную литературу, советую объем воды посмотреть в НТС 62-91-6, который называется Таблица справочных данных для стальных труб тепловых сетей, в столбике под названием – объем воды в 1 п.м. трубы. В этой же таблице указана масса воды в 1 п.
м. трубы.
Если у Вас, все же возникает вопрос, как определяется масса воды, то и здесь нет никаких тайн.
Масса воды равна (кг) = объем воды (м3) умножаете на 1000. Следовательно, вес 1 куба воды равен 1 тонне — 1 м3 = 1 тонна.
А теперь ответы на вопросы:
1 миллилитр сколько литров? Ответ очень прост. 1 миллилитр = 0,001 литра.
Сколько литров в кубическом метре? Ответ также прост. 1 м3 = 1000 литров. Кубический метр – это же просто объёму куба с длиной рёбер в 1 метр.
А как вы считаете объем воды в трубе или объем цилиндра, может уже что-то новое открыли?
Если Вам интересно, то 1 баррель нефти равен почти 159 литров, а если быть более точным, то 158,987 литра. Надеюсь, Вы теперь знаете ВСЁ! Сколько весит 1 л воды? Сколько в тонне литров?
Поделиться ссылкой:
Как рассчитать объём воды в трубе системы отопления, и не только.
Опубликовано: 28 декабря 2012 г.
Здравствуйте! Для того, чтобы правильно спроектировать систему отопления, нужно иметь о ней как можно больше исходной информации: площадь помещений, объём помещений, материал из которого изготовлены стены, степень теплоизоляции и т. д. Я хочу обратить Ваше внимание на один из таких факторов, как объём воды в трубах системы отопления. Как рассчитать объём воды в трубе, ведь для того, чтобы правильно подобрать мощность котла, необходимо обязательно знать объём воды в системе отопления, плюс, объём воды в котле!
Чтобы справиться с этой задачей нам нужно знать сколько метров трубы в системе отопления, причём каждого диаметра, т. е., сколько трубы диаметром 20 мм., сколько трубы диаметром 25 мм., и т. д.
Для чего это нужно? Сейчас Вы сами всё поймёте.
Взгляните на картинку снизу. В этой таблице представлены основные используемые в бытовых системах отопления диаметры труб, а так же объём воды в этих трубах.
Как не трудно догадаться, остаётся количество метров, каждого диаметра, помножить на объём воды, согласно таблицы. Затем полученный результат суммируем, и прибавляем объём воды в котле.
В паспорте каждого котла, имеются данные о максимальном объёме воды в системе отопления, который котёл может нагревать без потери мощности. Например: ваш котёл, по паспорту имеет мощность — 20 Квт., и допустимый объём теплоносителя — 180 литров. После подсчётов, у Вас получился объём воды в трубах равный — 220 литров. Что из этого следует? А то что если у вас площадь помещений например 120-150 кв. м., то котёл скорее всего справится с нагревом системы, а если площадь 180-200 кв. м., то всё, — зимой, в более сильный мороз придётся мёрзнуть. В таком случае вам нужен котёл большей мощности, например — 24 Квт. (Надеюсь вы понимаете, что эти цифры условные!)
Надеюсь, при расчёте системы отопления, эта информация поможет Вам избежать ненужных проблем!
Хочу добавить, что на картинке, объём воды в секции радиатора, имеется в виду чугунный радиатор.
В алюминиевых радиаторах, в одной секции объём жидкости составляет приблизительно 300гр., в зависимости от моделей.
Эту табличку можете скачать с моего сайта по этой ссылке:Таблица колличества воды, в одном метре трубы, по диаметрам
Ну вот и всё! Пользуйтесь на здоровье.
Сколько воды в 16 сшитом полиэтилене
Расчет объема трубы
Проектирование системы отопления, водопровода и даже канализации часто требует провести точный расчет объема трубы, и как это сделать, а главное, зачем это делать, знают не все. Прежде всего, объём трубы позволяет выбрать нужное отопительное или насосное оборудование, резервуары для воды или теплоносителя, просчитать габариты, которые будет занимать система трубопроводов, что в условиях тесных или подвальных помещений важно. Также объем теплоносителей может сильно отличаться из-за разной плотности жидкостей, поэтому и диаметры труб для води и, например, антифриза, могут быть разными.
Плюсы и минусы
Ни один из материалов не является идеальным, и имеет свои минусы.
Однако есть в списке и такие материалы, свойства которых вынуждают их покинуть рынок. Для отопления практически не используется ПВХ из-за низкой предельной температуры эксплуатации.
Недалеко ушел от него, по той же причине, полипропилен. Фактическими кандидатами на то, какие трубы выбрать для отопления, являются:
Металлопластик
Пресс-фитинг для металлопластика
Это материал с очень высокими эксплуатационными характеристиками (если имеет надлежащее качество). У него практически самое низкое сопротивление водному потоку. Он прост в монтаже и выдерживает температуры 90-100, а в кратковременных скачках – 110-130 °С, которые в индивидуальных системах отопления практически нереальны.
Дополнительное преимущество – его гибкость. Помимо того, что его можно спрятать в стенах или за мебелью, он позволяет прокладывать длинные бесстыковые участки произвольной формы, с любыми поворотами. Этим не может похвастаться ни один из прочих материалов.
Формулы расчетов
Самый простой способ рассчитать объем трубы – воспользоваться онлайн сервисом или специальной десктопной (настольной) программой.
Второй способ – вручную, и для этого понадобится обычный калькулятор, линейка и штангенциркуль, которым измеряют внутренний и наружный радиусы трубы (на всех чертежах и схемах радиус обозначается символом R или r). Можно воспользоваться значением диаметра (D или d), который вычисляется по простой формуле: R x 2 или R 2 . Чтобы вычислить объем воды в трубе в кубах, также понадобится узнать длину цилиндра L (или l).
Измерение внутреннего радиуса позволит узнать, сколько воды или другой жидкости в цилиндре. Результат отражается в кубических метрах. Знать наружный диаметр трубы необходимо для расчета габаритов того места, где будет прокладываться трубопровод.
Последовательность расчетов такова: сначала узнаю́т площадь сечения трубы:
- S = R x ∏;
- Площадь цилиндра – S;
- Радиус цилиндра – R;
- ∏ – 3,14159265.
Результат S умножают на длину L трубы – это и будет полный рассчитанный объем. Расчет объема по сечению и длине цилиндра выглядит так:
- Vтр = Sтр x Lтр;
- Объем цилиндра – Vтр;
- Площадь цилиндра – Sтр;
- Длина цилиндра – Lтр.
Пример:
- Стальная труба Ø = 0,5 м, L = 2 м;
- Sтр = (Dтр / 2) = ∏ х (0,5 / 2) = 0,0625 м 2 .
Конечная формула, как рассчитать объем трубы, будет выглядеть следующим образом:
V = H х S = 2 х 0,0625 = 0,125 м 3 ;
H – толщина стенки трубы.
Толщина стенок любой трубы
» alt=»»> Эта формула позволяет узнать, как посчитать объем трубы с любыми заданными параметрами и из любого материала, а также отдельные участки составного трубопровода. Чтобы не путаться в параметрах результатов, необходимо сразу выражать их в одних и тех же единицах, например, в метрах и кубических метрах, или в сантиметрах и кубических сантиметрах. Из компьютерных программ для начинающих пользователей или для тех, кто предполагает проводить одноразовые расчеты, можно предложить VALTEC.PRG, Unitconverter, Pipecalc и другие.
Как вычислить площадь поперечного сечения трубы
Для круглой трубы площадь поперечного сечения рассчитывается с использованием площади круга по следующей формуле:
Где:
- R – внутренние радиус трубы;
- ∏ – постоянная величина 3,14.
Sтр Ø = 90 мм, или R = 90 / 2 = 45 мм или 4,5 см. Согласно формуле, Sтр = 2 х 20,25 см 2 = 40,5 см 2 , где 20,25 – это 4,5 см в квадрате.
Параметры трубопровода
Площадь сечения профилированной трубы Sпр нужно рассчитывать по формуле, применяемой для вычисления площади прямоугольной фигуры:
a и b – стороны прямоугольной профилированной трубы. При сечении трубопровода 40 х 60 мм параметр Sпр = 40 мм х 60 мм = 2400 мм 2 (20 см2, или 0,002 м2).
Как рассчитать объем воды в водопроводной системе
Для расчета объема трубы в литрах в формулу следует подставлять внутренний радиус, но это не всегда возможно, например, для радиаторов сложной формы или расширительной емкости с перегородками, для отопительного котла. Котел отопления.
Поэтому сначала нужно узнать объем изделия (обычно из технического паспорта или другой сопроводительной документации). Так, у чугунного стандартного радиатора объем одной секции равен 1,5 л, для алюминиевых – в зависимости от конструкции, вариантов которых может быть достаточно много.
Геометрические параметры алюминиевых радиаторов
Узнать объем расширительного бачка (как и других нестандартных емкостей любого назначения) можно, залив в него заранее измеренный объем жидкости. Для подсчетов объема любой трубы нужно измерить ее диаметр, затем вычислить объем одного погонного метра, и умножить результат на длину трубопровода.
В справочной литературе, предназначенной для регламентирования параметров труб, приведены таблицы со значениями, которые нужны для расчетов объемов труб и других изделий. Эта информация является ориентировочной, но достаточно точной для того, чтобы использовать ее на практике. Выдержка из такой таблицы приведена ниже, и она пригодится для домашних расчетов:
| Ø внутр, мм | Vвнутр 1 погонного метра трубы, л | Vвнутр 10 погонных метров трубы, л |
| 4,0 | 0,0126 | 0,1257 |
| 5,0 | 0,0196 | 0,1963 |
| 6,0 | 0,0283 | 0,2827 |
| 7,0 | 0,0385 | 0,3848 |
| 8,0 | 0,0503 | 0,5027 |
| 9,0 | 0,0636 | 0,6362 |
| 10,0 | 0,0785 | 0,7854 |
| 11,0 | 0,095 | 0,9503 |
| 12,0 | 0,1131 | 1,131 |
| 13,0 | 0,1327 | 1,3273 |
| 14,0 | 0,1539 | 1,5394 |
| 15,0 | 0,1767 | 1,7671 |
| 16,0 | 0,2011 | 2,0106 |
| 17,0 | 0,227 | 2,2698 |
| 18,0 | 0,2545 | 2,5447 |
| 19,0 | 0,2835 | 2,8353 |
| 20,0 | 0,3142 | 3,1416 |
| 21,0 | 0,3464 | 3,4636 |
| 22,0 | 0,3801 | 3,8013 |
| 23,0 | 0,4155 | 4,1548 |
| 24,0 | 0,4524 | 4,5239 |
| 26,0 | 0,5309 | 5,3093 |
| 28,0 | 0,6158 | 6,1575 |
| 30,0 | 0,7069 | 7,0686 |
| 32,0 | 0,8042 | 8,0425 |
Параметры пластиковых труб
Материал, из которого изготавливаются трубы для водопровода или канализации, может быть разным, соответственно, характеристики труб тоже будут отличаться.
Стальные трубы, например, которые имеют большой внутренний диаметр, пропустят намного меньшее количество воды, чем аналогичные трубы из пластика или пропилена.
Это происходит из-за разной гладкости внутренней поверхности трубы – у железных изделий она намного меньше, а ППР и ПВХ трубы не имеют шероховатостей на внутренних поверхностях. Но металлические трубы помещают в себя больший объем жидкости, чем изделия из других материалов с одинаковым внутренним сечением. Поэтому все расчеты для труб из разных материалов необходимо проверять, и сделать это можно как в онлайн калькуляторе, так и в настольной компьютерной программе, специально для этого предназначенной.
Десктопная программа для расчетов объема
| Условный проход | Наружный диаметр | Толщина стенки труб | Масса 1 м труб, кг | ||||
| Легких | Обыкновенных | Усиленных | Легких | Обыкновенных | Усиленных | ||
| 6 | 10,2 | 1,8 | 2,0 | 2,5 | 0,37 | 0,40 | 0,47 |
| 8 | 13,5 | 2,0 | 2,2 | 2,8 | 0,57 | 0,61 | 0,74 |
| 10 | 17,0 | 2,0 | 2,2 | 2,8 | 0,74 | 0,80 | 0,98 |
| 15 | 21,3 | 2,35 | – | – | 1,10 | – | – |
| 15 | 21,3 | 2,5 | 2,8 | 3,2 | 1,16 | 1,28 | 1,43 |
| 20 | 26,8 | 2,35 | 1,42 | – | |||
| 20 | 26,8 | 2,5 | 2,8 | 3,2 | 1,50 | 1,66 | 1,86 |
| 25 | 33,5 | 2,8 | 3,2 | 4,0 | 2,12 | 2,39 | 2,91 |
| 32 | 42,3 | 2,8 | 3,2 | 4,0 | 2,73 | 3,09 | 3,78 |
| 40 | 48,0 | 3,0 | 3,5 | 4,0 | 3,33 | 3,84 | 4,34 |
| 50 | 60,0 | 3,0 | 3,5 | 4,5 | 4,22 | 4,88 | 6,16 |
| 65 | 75,5 | 3,2 | 4,0 | 4,5 | 5,71 | 7,05 | 7,88 |
| 80 | 88,5 | 3,5 | 4,0 | 4,5 | 7,34 | 8,34 | 9,32 |
| 90 | 101,3 | 3,5 | 4,0 | 4,5 | 8,44 | 9,60 | 10,74 |
| 100 | 114,0 | 4,0 | 4,5 | 5,0 | 10,85 | 12,15 | 13,44 |
| 125 | 140,0 | 4,0 | 4,5 | 5,5 | 13,42 | 15,04 | 18,24 |
| 150 | 165,0 | 4,0 | 4,5 | 5,5 | 15,88 | 17,81 | 21,63 |
Если схема вашего трубопровода имеет свою специфику, рассчитать точные параметры для требуемого расхода жидкости можно по формулам, которые приведены выше.
» alt=»»>
Источник
Расход воды через трубу при нужном давлении
Содержание статьи
Основная задача расчёта объёма потребления воды в трубе по её сечению (диаметру) – это подобрать трубы так, чтобы водорасход не был слишком большой, а напор оставался хороший. При этом необходимо учесть:
- диаметры (ДУ внутреннего сечения),
- потери напора на рассчитываемом участке,
- скорость гидропотока,
- максимальное давление,
- влияние поворотов и затворов в системе,
- материал (характеристики стенок трубопровода) и длину и т.д..
Подбор диаметра трубы по расходу воды с помощью таблицы считается более простым, но менее точным способом, чем измерение и расчёт по давлению, скорости воды и прочим параметрам в трубопроводе, сделанный по месту.
Рынок материалов
Все существующие трубопроводные системы можно разделить на две большие группы:
Металлические
- «Черный» металл
- Нержавеющая сталь
- Медь, латунь, бронза
Гораздо реже используется оцинкованная сталь, в единичных случаях – титан, алюминий, прочие цветные металлы и сплавы.
Полимерные
- Полипропилен
- Полиэтилен
- Металлопластик
- ПВХ
При этом в группе полимеров на самом деле структура гораздо сложнее этой простой классификации. Ведь помимо того, что каждый материал сам по себе имеет по нескольку модификаций, он еще может иметь несколько слоев.
Для металлопластиковых труб для отопления это понятно из его названия, но и здесь все не так просто. Это – трехслойный материал из алюминиевой фольги, расположенной между двумя слоями полимера.
Сам же материал – это либо сшитый полиэтилен (PEX), либо – полипропилен (PP), но и в каждом из этих случаев еще существует по нескольку разновидностей, зависящих от способа изготовления пластика и его класса.
Металлопластиковые трубы на основе полиэтилена
Табличные стандартные данные и средние показатели по основным параметрам
Для определения расчётного максимального расхода воды через трубу приводится таблица для 9 самых распространённых диаметров при различных показателях давления.
Среднее значение давления в большинстве стояках находится в интервале 1,5-2,5 атмосфер. Существующая зависимость от количества этажей (особенно заметная в высотных домах) регулируется путём разделения системы водообеспечения на несколько сегментов. Водонагнетение с помощью насосов влияет и на изменение скорости гидропотока. Кроме того, при обращении к таблицам в расчёте водопотребления учитывают не только число кранов, но и количество водонагревателей, ванн и др. источников.
Изменение характеристик проходимости крана с помощью регуляторов водорасхода, экономителей, аналогичных WaterSave ( https://water-save.com/ ), в таблицах не фиксируются и при расчёте расхода воды на (по) трубе, как правило, не учитываются.
Инструментальный вопрос
Если монтировать систему своими руками, не последнюю роль в том вопросе, какую трубу для отопления выбрать, может сыграть необходимый инструмент. Ведь практически каждый из видов труб требует для установки специфического инвентаря, при этом весьма недешевого.
При этом даже если есть пресс-фитинги от какого-либо производителя, не факт, что опрессовщик другой фирмы позволит качественно их обжать. То же самое касается паяльных аппаратов для полиэтилена. А это значит, что, возможно, взять оснастку в аренду не удастся.
Для пайки тех же медных труб требуются весьма специфические навыки и четкое знание технологии производства работ, так что браться за эту операцию без соответствующей квалификации специалисты не рекомендуют.
Паяльник для полиэтиленовых труб
Есть свои нюансы и в сварке полиэтилена. Все эти моменты также следует обдумать и учесть, перед тем, как выбрать трубы для отопления окончательно. В этом смысле наиболее демократичной системой является соединение на разрезных кольцах, его также называют «О-ринг».
Способ транспортировки жидкости по трубопроводу и устройство для его реализации — Транспортировка и хранение
Описан и обоснован способ транспортировки жидкости (газа) по трубопроводу за счёт энергии состояния транспортируемой жидкости.
С помощью представленного устройства создаётся устойчивое состояние вращательного движения масс транспортируемой жидкости, которая формирует в трубопроводе вихревую трубку. В результате передачи внешнего возбуждения в зону вихревой трубки появляется компонента нормально осевого перемещения жидкости, вращательное движение переходит в винтовое движение. При этом, компонента вращательного (потенциального) движения значительно превосходит компоненту нормального перемещения, что создаёт эффект сверхтекучести транспортируемой жидкости. При этом, внешняя энергия расходуется исключительно на поддержание заданного состояния системы, а не на перемещение транспортируемых масс, как в существующих системах.
В этой статье представлено научно-обоснованное техническое решение по транспортировке жидкости (газа) по трубопроводам за счёт энергии самой жидкости.
В 1938 г. П.Л. Капица открыл, а Л.Д. Ландау в 1941 году научно обосновал, явление сверхтекучести квантовой жидкости.
Сверхтекучесть характеризуется не только способность протекания квантовой жидкости через тончайшие капилляры без сопротивления, но и способностью самостоятельно подниматься по ним, вопреки гравитации. Ландау объяснил сверхтекучее свойство квантовой жидкости наличием в ней сверхтекучей компоненты. При этом сверхтекучесть проявляется лишь в случае, когда сверхтекучая компонента преобладает над нормальной. Говоря о нормальной и сверхтекучей компоненте необходимо иметь ввиду, что речь идёт исключительно о разных видах движения. «Следует, однако, самым решительным образом подчеркнуть, что рассмотрение жидкости как смеси нормальной и сверхтекучей её частей является не более чем способом наглядного описания явлений, происходящих в квантовых жидкостях. … В действительности надо говорить, что в квантовой жидкости – He ΙΙ – может существовать одновременно два движения, каждое из которых связано со своей эффективной массой (так что сумма обеих этих масс равна полной истинной массе жидкости)». [1] Для объяснения сверхтекучести Ландау использовал аналогию с твёрдым телом.
В естественном ряде состояний между твёрдым телом и квантовой жидкостью остался пробел – нормальная вязкая жидкость, к которой относятся и газ, и вода, и нефть. Для придания нормальной жидкости свойств сверхтекучей жидкости, необходимо создание в ней, преимущественно, сверхтекучей компоненты.
По своей сути сверхтекучая компонента ничто иное, как свободное (собственное) вращательное движение жидкости – ротон (от лат. roto — вращаюсь, верчусь). В теории сверхтекучести, ротон – элементарное возбуждение (квазичастица). «Подчёркиваем, что хотя мы говорим здесь о «частице», но её «элементарность» нигде не используется. Поэтому полученные формулы в равной степени применимы и к любому сложному телу, состоящему из многих частиц…». [2] Создание в вязкой жидкости свободного вращательного движения задача элементарная. На рисунке (фиг. 1) представлена принципиальная схема «устройства для генерирования реактивного импульсного потока газа или жидкости», где Ι – блок аккумулирования вращательного движения масс рабочего тела, ΙΙ – блок компрессии, ΙΙΙ – усилитель, 4 – полый ротор, 5 – статор, 6 – токопроводящая обмотка статора, 7 – пассивная обмотка статора, 8 – корпус, 9 – пассивный ротор.
Такое название устройства обусловлено его двойным назначением. В трубопроводах нет надобности получать реактивный поток, в общепринятом понимании относящимся к двигателям.
Фиг. 1. Принципиальная схема «устройства для генерирования реактивного импульсного потока газа или жидкости»
Ι – блок аккумулирования вращательного движения масс рабочего тела, ΙΙ – блок компрессии, ΙΙΙ – усилитель, 4 – полый ротор, 5 – статор, 6 – токопроводящая обмотка статора, 7 – пассивная обмотка статора, 8 – корпус, 9 – пассивный ротор.
На токопроводящую обмотку статора (6) блока аккумулирования (Ι ) подаётся электрический импульсный ток, фиксированный по величине и продолжительности, переменный по частоте, для чего используется частотно-импульсный преобразователь. Разгоняется ротор равноускоренно, для чего частота тока возрастает пропорционально росту собственной частоты вращения ротора. Присоединение масс жидкости может происходить только при переменном (ускоренном) движении.
При этом движение должно быть равноускоренным с небольшой фиксированной величиной ускорения. Только при соблюдении этого условия возможно формирование устойчивого состояния рабочего тела и постоянной энергии состояния. «Изменение состояния (или положения) одной из частиц приводит к изменению создаваемого ею поля, которое отражается на другой частице лишь через конечный промежуток времени, необходимый для распространения этого изменения до частицы». [3] Полученное состояние представляет собой вихревую трубку. Энергия состояния жидкости в вихревой трубке, являющаяся суммой её кинетической и внутренней энергий, является функцией собственной угловой скорости. Вывод: величина собственной угловой скорости определяет физическое состояние жидкости. Описывая свободное вращательное движение, Л. Ландау подчёркивает его обязательную потенциальность, которая выражается равенством rot vs= 0, «которое должно иметь место в любой момент времени во всём объёме жидкости». [4] Потенциальность означает, что при вращательном движении не совершается работа.
Поэтому вращательное движение не процесс, а состояние. Поэтому давление жидкости на стенки сосуда (трубы) стремится к нулю, при минимуме нормальной компоненты, наличие которой определяет существование процесса. Фактически, давление на стенки трубы и величина трения зависят от соотношения величин вращательного движения и поступательного перемещения жидкости. Вообще аккумулирующее свойство вращательного движения известно с древности. Аккумулируется именно движение, массы, вовлечённые во вращательное движение, являются присоединёнными и, по своей сути, вторичны. Это состояние является устойчивым (атом, космос). В предлагаемом решении его можно считать квазиустойчивым. Формирование состояния жидкости первый этап осуществления способа.
Особое значение в вихревой теории имеют теоремы Гельмгольца, которые Пуанкаре считал наиболее значительным вкладом в гидродинамику. Их сутью является закон «вмороженности вихревых линий», позволяющий рассматривать «вихревые образования» как некоторые «материальные объекты, подобные массам в классической механике».
И, что перемещение вращающихся масс всегда перпендикулярно их плоскости вращения. В трубе перемещение происходит по оси трубы, являющейся осью вращения.
Переход от чисто вращательного движения к вращательно-поступательному, винтовому, происходит под действием внешнего возбуждения на поле вращения. Для чего на токопроводящую обмотку (6) статора усилителя или аккумулятора, в зависимости от конкретных режимов, подаётся импульсный ток возбуждения. По своей сути этот переход представляет собой вынужденное излучение.
Для понимания процесса необходимо вновь обратиться к аналогии (этот метод аналогий при доказательстве своих теорий сверхтекучести и вынужденного излучения использовали Ландау и Эйнштейн, соответственно). «Вынужденное излучение (вынужденное испускание, индуцированное излучение), испускание электромагнитного излучения квантовыми системами под действием внешнего (вынуждающего) излучения». [5] Согласно постулированной Эйнштейном теории вынужденного излучения, вынужденное излучение – процесс обратный поглощению, которые равны при соблюдении определённого условия – соблюдения критической частоты внешнего возбуждения.
Так, в частности, работает квантовый усилитель. Критическая величина частоты внешнего возбуждения (n) определяется частотой собственных (свободных) колебаний системы (ω/2π) и должна соответствовать условию n ≤ ω/2π, где ω – собственная угловая скорость. При нарушении приведённого условия, превышении частоты внешнего возбуждения над частотой собственных колебаний, происходит разрушение поля вращения – вихревой трубки. Способность к релаксации поля вращения, сохранение заданного состояния и его характеристик, обусловлено наличием собственного спина, что является важнейшим отличием предлагаемого способа от известных, определяющим его уникальность и эффективность. Релаксация, в данном случае, есть процесс поглощения, обратный и равный по величине генерированию (испусканию). Генерируемый объём жидкости одновременно замещается равным объёмом жидкости, исходное состояние которого практически соответствует состоянию жидкости в поле вращения, так как является частью вихревой трубки. Фактически речь идёт не о присоединённых массах, а о присоединённом вихре.
Внешняя энергия, передаваемая полю вращения с внешним возбуждением, расходуется не на перемещение объёмов (масс) жидкости, а на поддержание заданного состояния, на поддержания равновесия системы, которое является квазиустойчивым. Перемещение же осуществляется за счёт энергии состояния жидкости в вихревой трубке, представляющей сумму кинетической и внутренней энергий жидкости, что не противоречит принципам работы инерционных систем и первому началу термодинамики. Перемещение, в определённой мере, можно считать «побочным» следствием внешнего возбуждения.
Полученное состояние поля вращения присоединённых масс уникально. Оно одновременно является и устойчивым, и возбуждённым. И устойчивость, и возбуждённость являются функцией одной величины – угловой скорости. Она, угловая скорость, через частоту вращения, определяет и линейную скорость перемещения жидкости по трубе, характеристики импульсного потока. Статистика такого процесса отсутствует, её ещё придётся набирать. Поэтому необходимо, для расчёта производительности, обратиться к теории и аналогии.
Уже говорилось, что каждая компонента движения связана со своей эффективной массой. В рассматриваемом состоянии присутствует только вращательное движение эффективную массу которого, по аналогии с квантовой жидкостью, можно принять равной mэ ≈ 3,08 m0. [6] Это соответствует и логической модели, где плотность жидкости в кольце тора значительно выше её нормальной плотности, но объём занимаемый жидкостью это лишь малая часть объёма трубы. Скорость линейного перемещения жидкости определяется на основе представления, что движение является сложным, винтовым. Учитывая ничтожность величины диаметра трубы относительно линейной скорости вращения, можно принять v ≈ vs = aω, где v – линейная скорость перемещения жидкости по трубе. С появлением линейного перемещения жидкости появляется нормальная компонента движения, что отрицательно влияет на текучесть жидкости. Для снижения этого влияния необходимо руководствоваться «принципом наименьшего действия», а объёмы перемещения, производительность процесса, регулировать частотой внешнего возбуждения.
Теперь можно вывести формулу плотности потока жидкости (Р) в трубе: Р ≈ mэ vпτ или Р ≈ ρVaωпτ, где ρ – плотность жидкости, V – объём жидкости, a – расстояние от оси вращения до центра масс, п(1/с) – частота внешнего возбуждения в единицу времени → ω/2π; τ(с) – период (продолжительность) вынужденного излучения. Величина mэ v ≈ ρVaω является величиной единичного импульса (р), тогда Р = рпτ. Объём единичного импульса определяется объёмом полости ротора в зоне генерирования и собственной угловой скоростью, и представляет, по аналогии, квазичастицу конкретного поля, его «наименьшее действие».
Величина импульса внешнего возбуждения, обеспечивающая ускоренное вращение ротора до достижения заданной величины угловой скорости (частоты собственных колебаний), определяется по принципу «минимальной достаточности» (наименьшего принуждения) и полностью зависит от характеристик конструкции устройства и транспортируемой жидкости. Величина внешнего возбуждения генерирования потока не должна превышать величину «разгонного» возбуждения.
Частота собственных (свободных) колебаний системы (частота вращения ротора) определяет эффективность её работы. «…В среде конечного объёма могут происходить свободные колебания лишь с вполне определёнными частотами. …Конкретные значения собственных частот зависят от формы и размеров сосуда. В каждом данном случае существует бесконечный ряд возрастающих собственных частот. Нахождение их требует конкретного исследования уравнения движения с соответствующими граничными условиями». [7] Речь идёт о множественности собственных энергетических уровней состояния, их «бесконечном» ряде. Эффективность способа обратно пропорциональна диаметру трубопровода, то есть чем меньше диаметр трубы, тем более эффективно работает система. И дело здесь не только и не столько в стоимости самого трубопровода, а в характеристиках процесса. Малый диаметр трубы позволяет получать бόльшие угловые скорости, что означает преимущество сверхтекучей компоненты и, одновременно с ростом собственной частоты, более высокую частоту импульсов потока.
Реализация представленного способа позволит, по приближённым расчетам автора, повысить пропускную способность существующих и проектируемых трубопроводов, как минимум, в десятки раз, значительно снизив при этом капитальные, эксплуатационные и энергетические затраты. Ещё одним важнейшим преимуществом предлагаемого способа транспортировки жидкости является возможность регулирования температуры транспортируемой жидкости по длине трубы. Это достигается без дополнительных капитальных затрат путём чередования режимов «нагнетания» и «откачки», генерированием потока через устройства на входе и выходе соответственно.
Способ и устройство для его реализации защищены патентами РФ. Начата процедура получения иностранных патентов.
1. Ландау, Лифшиц, «Гидродинамика», 2006 г., с. 705
2. Ландау, Лифшиц, «Теория поля», 2006 г., с. 47
3. БСЭ, Поля физические
4. Ландау, Лифшиц, «Гидродинамика», 2006 г., с. 707
5.
Физический энциклопедический словарь, «Вынужденное излучение»
6. Физический энциклопедический словарь, « Эффективная масса»
7. Ландау, Лифшиц, «Гидродинамика», 2006 г., с. 373
Трубы с содержанием воды — вес и объем
| Размер трубки (внутри диаметра) (в) (в) 2 3 Содержание воды |
| ||||||
|---|---|---|---|---|---|---|---|
| Объем | Вес (LB / FT) |
Объем / вес | |||||
| (в 3 / Ft) | (галлоны / фут) | (литр / м, кг / м) | |||||
| 1 / 4 | 0.59 | от 0,003 0,02 0,030 | |||||
| 3/8 1.33 | 0,006 | 0,05 | |||||
| 1/2 2,36 | 0,010 0,09 | 0,13 | |||||
| 3/4 | 5/4 | 5. 30 |
0.023 | 0.28 | 0.28 | ||
| 1 | 1 | 9.43 | 0.041 | 0.041 | 0.34 | 0.51 | |
| 1 1/4 | 14. | 7 0,064 | 0,53 0,79 | ||||
| 21,2 | 0,092 0,77 | 1,1 | |||||
| 2 37,7 | 0,163 1,36 | 2.0 | |||||
| 2 1/2 | 58.9 | 0.255 | 0.255 | 2.13 | 3.2 | ||
| 3 | 84,8 | 84,8 | 0.367 | 2.31 | 3.4 | ||
| 4 | 150.8 | 0,653 | 5,44 | 8,1 | |||
| 5 | 235,6 | 1,02 | 8,50 | 13 | |||
| 6 | 339,3 | 1,47 | 12,2 | 18 | |||
| 8 | 603.2 | 2.61 | 21.61 | 21. 8 |
32 | ||
| 10 | 942.5 | 942.5 | 4,08 | 4,08 | 34.0 | 51 | |
| 12 | 1357.2 | 5,88 | 49,0 | 73 | |||
| 15 | 2120,6 | 9,18 | 76,5 | 114 | |||
- 1 фунт / фут = 1,49 кг / м
- 1 галлон ( США)/фут = 12,4 л/м
Обратите внимание, что для большинства труб номинальный размер не равен внутреннему диаметру. Чтобы узнать точные объемы, сверьтесь с документацией или стандартом на трубу и воспользуйтесь калькулятором ниже.
Объемный вес других жидкостей можно рассчитать с учетом плотности.
Пример – Содержание воды в трубе
Объем воды в трубе 12 м длиной 2 дюйма можно рассчитать как
(2,0 л/м) (12 м)
литр.
Трубы — Калькулятор объема
Этот калькулятор можно использовать для расчета объема воды или других жидкостей в трубах.
Калькулятор является универсальным и может использоваться для любых единиц измерения, если они используются последовательно.Если введено значение м результат м 3 /м и так далее.
Внутренний диаметр трубы (м, мм, фут, дюйм…)
Для других единиц измерения используйте конвертер объема в левой колонке.
Калькулятор объема трубы
Как найти объем трубы?
Цилиндр представляет собой трехмерное тело с конгруэнтными основаниями в паре параллельных плоскостей. Эти основания представляют собой конгруэнтные окружности. Осью цилиндра называется отрезок с концами в центрах оснований.
Высота или высота цилиндра, обозначаемая $h$, представляет собой перпендикулярное расстояние между его круглыми основаниями.
В дальнейшем мы будем рассматривать только правый цилиндр, т.е. цилиндр, в котором ось и высота совпадают. Труба или трубка представляет собой полый цилиндр. Полый цилиндр — это цилиндр, который пуст изнутри, а его основание имеет внутренний и внешний радиусы.
Полый цилиндр имеет основание в виде кольца. Примеры полых цилиндров: трубы, круглые здания, соломинки и т. д.
Объем трубы — это мера объема пространства, которое занимает труба. Другими словами, объем материала, необходимого для изготовления трубы.3$$
Работа с объемом трубы с шагами показывает полный пошаговый расчет для нахождения объема внутри трубы с длиной внутреннего радиуса $10\;дюйм$ и высотой $8\;дюйм$ по формуле объема. Для любых других значений радиусов основания и высоты трубы просто укажите три положительных действительных числа и нажмите кнопку «Создать работу». Учащиеся начальной школы могут использовать этот калькулятор объема трубы для выполнения работы, проверки результатов объема трехмерных тел или эффективного решения домашних задач.
Формула скорости потока
Скорость потока жидкости — это мера объема жидкости, перемещающегося за определенное время. Скорость потока зависит от площади трубы или канала, по которому движется жидкость, и скорости жидкости.
Если жидкость течет по трубе, площадь равна A = πr 2 , где r — радиус трубы. Для прямоугольника площадь равна A = wh , где w — ширина, а h — высота.Скорость потока может быть измерена в кубических метрах в секунду ( м 3 /с ) или в литрах в секунду ( л/с ). Литры чаще используются для измерения объема жидкости, и 1 м 3 /с = 1000 л/с .
расход жидкости = площадь трубы или канала × скорость жидкости
Q = Ав
Q = расход жидкости ( м 3 /с или л/с )
А = площадь трубы или канала ( м 2 )
v = скорость жидкости ( м/с )
Формула расхода Вопросы:
1) Вода течет по круглой трубе радиусом 0.0800 м . Скорость воды 3,30 м/с . Каков расход воды в литрах в секунду ( л/с )?
Ответ: Скорость потока зависит от площади круглой трубы:
А = πr 2
А = π(0,0800 м) 2
А = π(0,00640 м 2 )
А = 0,0201 м 2
Площадь трубы 0,0201 м 2 .
Расход можно найти в м 3 /с по формуле:
Q = Ав
Q = (0,0201 м 2 )(3,30 м/с)
Q = 0,0663 м 3 /с
Расход можно преобразовать в литры в секунду, используя: 1 м 3 /с = 1000 л/с.
Q = 66,3 л/с
Расход воды по круглой трубе 66,3 л/с.
2) Вода стекает по открытому прямоугольному желобу. Желоб имеет ширину 1,20 м , а глубина стекающей в него воды 0,200 м . Скорость воды определяется по круглой трубе радиусом 0,0800 м . Скорость воды 5,00 м/с . Каков расход воды через желоб в литрах в секунду ( л/с) ?
Ответ: Расход зависит от площади желоба, через который проходит вода:
А = белый
А = (1.20 м)(0,200 м )
А = 0,240 м 2
Площадь воды, протекающей по желобу, равна 0,240 м 2 .
Расход можно найти в м 3 /с по формуле:
Q = Ав
Q = (0,240 м 2 )(5,00 м/с)
Q = 1,20 м 3 /с
Скорость потока можно преобразовать в литры в секунду, используя:
1 м 3 /с = 1000 л/с.
Q = 1200 л/с
Расход воды в желобе 1200 л/с .
Поток в трубе
Средняя скорость потока жидкости и диаметр трубы для известного расхода
Скорость жидкости в трубе неравномерна по площади сечения. Поэтому используется средняя скорость, и она рассчитывается по
уравнение неразрывности для установившегося потока в виде:
Калькулятор диаметра трубы
Рассчитайте диаметр трубы для известного расхода и скорости.
Рассчитайте скорость потока для известного диаметра трубы и скорости потока.
Преобразование объемного расхода в массовый.
Рассчитайте объемный расход идеального газа при различных условиях давления и температуры.
Диаметр трубы можно рассчитать, если объемный расход и скорость известны как:
где: D — внутренний диаметр трубы; q — объемный расход;
v — скорость; А — площадь поперечного сечения трубы.
Если массовый расход известен, то диаметр можно рассчитать как:
где: D — внутренний диаметр трубы; w — массовый расход; ρ — плотность жидкости; v — скорость.
Рассчитайте диаметр трубы простым способом
Взгляните на эти
три простых примера
и узнайте, как с помощью калькулятора
рассчитать диаметр трубы для известного расхода жидкости и желаемого расхода жидкости.
Ламинарный и турбулентный режим течения жидкости в трубе, критическая скорость
Если скорость жидкости внутри трубы мала, то линии тока будут прямыми параллельными линиями. Так как скорость жидкости внутри
труба постепенно увеличивается, линии тока будут оставаться прямыми и параллельными стенке трубы, пока не будет достигнута скорость
когда линии тока будут колебаться и внезапно превращаться в рассеянные узоры.Скорость, с которой это происходит, называется
«критическая скорость». При скоростях выше «критических» линии тока случайным образом распределяются по трубе.
Режим течения, когда скорость ниже «критической», называется ламинарным течением (или вязким, или обтекаемым течением). В ламинарном режиме
потока скорость наибольшая на оси трубы, а на стенке скорость равна нулю.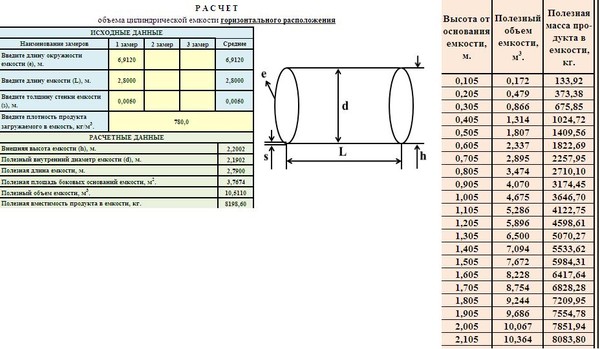
При скорости больше «критической» режим течения турбулентный. В турбулентном режиме течения неравномерно
беспорядочное движение частиц жидкости в направлениях, поперечных направлению основного потока. Изменение скорости турбулентного потока равно
равномернее, чем в ламинарном.
При турбулентном режиме течения у стенки трубы всегда имеется тонкий слой жидкости, движущийся ламинарно.Этот слой
называется пограничным слоем или ламинарным подслоем. Для определения режима течения используйте калькулятор чисел Рейнольдса.
Число Рейнольдса, турбулентное и ламинарное течение, скорость течения в трубе и вязкость
Характер течения в трубе согласно работе Осборна Рейнольдса зависит от диаметра трубы, плотности и вязкости.
текущей жидкости и скорости потока.Используется безразмерное число Рейнольдса, представляющее собой комбинацию этих четырех
переменными и может рассматриваться как отношение динамических сил массового потока к напряжению сдвига из-за вязкости.
Число Рейнольдса равно:
где: D — внутренний диаметр трубы; v — скорость; ρ — плотность;
ν — кинематическая вязкость; μ — динамическая вязкость;
Калькулятор числа Рейнольдса
Рассчитайте число Рейнольдса с помощью этого простого в использовании калькулятора.Определить, является ли течение ламинарным
или турбулентный. Применяется для жидкостей и газов.
Это уравнение можно решить с помощью
и калькулятор режима течения жидкости.
Течение в трубах считается ламинарным, если число Рейнольдса меньше 2320, и турбулентным, если число Рейнольдса
превышает 4000.Между этими двумя значениями находится «критическая» зона, где течение может быть ламинарным, турбулентным или в
процесс изменений и в основном непредсказуем.
При расчете числа Рейнольдса для эквивалентного диаметра некруглого поперечного сечения (четырехкратный гидравлический радиус d=4xRh)
используется, и гидравлический радиус может быть рассчитан как:
Rh = площадь поперечного сечения потока / смоченный периметр
Это относится к квадратным, прямоугольным, овальным или круглым трубопроводам, если они не имеют полного сечения.Из-за большого разнообразия жидкостей, используемых в современных промышленных процессах, одно уравнение
который можно использовать для потока любой жидкости в трубе, дает большие преимущества.
Это уравнение — формула Дарси,
но один фактор — коэффициент трения приходится определять экспериментально. Эта формула имеет широкое применение
в области гидромеханики и широко используется на этом веб-сайте.
Уравнение Бернулли — сохранение напора жидкости
Если пренебречь потерями на трение и к трубопроводной системе не добавляется и не отбирается энергия, общий напор H,
сумма напора, напора и скоростного напора будет постоянной для любой точки
потока жидкости.
Это выражение закона сохранения напора для потока жидкости в трубопроводе или линии тока, известное как
Уравнение Бернулли:
где: Z 1,2 — превышение над уровнем отсчета; р 1,2 — абсолютное давление;
v 1,2 — скорость; ρ 1,2 — плотность; г — ускорение свободного падения
Уравнение Бернулли используется в нескольких калькуляторах на этом сайте, например
калькулятор падения давления и расхода,
Расходомер с трубкой Вентури и калькулятор эффекта Вентури и
Калькулятор размера диафрагмы и скорости потока.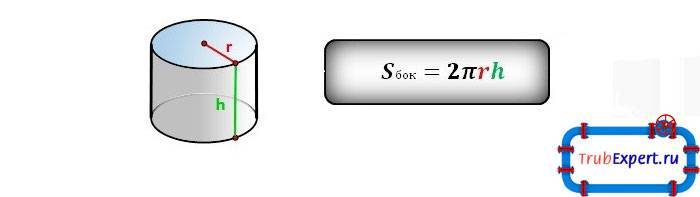
Течение в трубе и падение давления на трение, потеря энергии напора | Формула Дарси
Из уравнения Бернулли выводятся все другие практические формулы с модификациями, связанными с потерями и выигрышами энергии.
Как и в реальной системе трубопроводов, существуют потери энергии, и энергия добавляется к жидкости или забирается из нее.
(с использованием насосов и турбин) они должны быть включены в уравнение Бернулли.
Для двух точек одной линии тока в потоке жидкости уравнение можно записать следующим образом:
где: Z 1,2 — превышение над уровнем отсчета;
р 1,2 — абсолютное давление;
v 1,2 — скорость;
ρ 1,2 — плотность;
h L — потеря напора из-за трения в трубе;
Н р — головка насоса;
H T — головка турбинная;
г — ускорение свободного падения;
Течение в трубе всегда приводит к потерям энергии из-за трения.
Потеря энергии может быть измерена как падение статического давления.
в направлении потока жидкости двумя манометрами. Общее уравнение падения давления, известное как формула Дарси, выраженное
в метрах жидкости:
где:
h L — потеря напора из-за трения в трубе;
ф — коэффициент трения;
L — длина трубы;
v — скорость;
D — внутренний диаметр трубы;
г — ускорение свободного падения;
Чтобы выразить это уравнение как падение давления в ньютонах на квадратный метр (Паскалях), замена соответствующих единиц приводит к:
Калькулятор падения давления
Калькулятор на основе уравнения Дарси.
Рассчитать падение давления для известного расхода
или рассчитать скорость потока для известного перепада давления. Включен расчет коэффициента трения.
Подходит для ламинарного и турбулентного потока, круглого или прямоугольного воздуховода.
где:
Δ p — падение давления из-за трения в трубе;
ρ — плотность;
ф — коэффициент трения;
L — длина трубы;
v — скорость;
D — внутренний диаметр трубы;
Q — объемный расход;
Уравнение Дарси можно использовать как для ламинарного, так и для турбулентного режима течения и для любой жидкости в трубе.С некоторыми ограничениями,
Уравнение Дарси можно использовать для газов и паров.
Формула Дарси применяется, когда диаметр трубы и плотность жидкости постоянны и
труба относительно прямая.
Коэффициент трения для шероховатости трубы и число Рейнольдса при ламинарном и турбулентном течении
Физические значения в формуле Дарси очень очевидны и могут быть легко получены, когда известны свойства трубы, такие как D — внутренняя часть трубы.
диаметр, L — длина трубы и, когда известен расход, скорость можно легко рассчитать с помощью уравнения неразрывности.Единственное значение
что необходимо определить экспериментально, так это коэффициент трения. Для ламинарного режима течения Re < 2000 можно рассчитать коэффициент трения,
а для турбулентного режима течения, где Re > 4000, используются экспериментально полученные результаты.
В критической зоне, где Рейнольдс
число между 2000 и 4000, может возникнуть как ламинарный, так и турбулентный режим течения, поэтому коэффициент трения является неопределенным и имеет более низкую
пределы для ламинарного потока и верхние пределы, основанные на условиях турбулентного потока.
Если течение ламинарное и число Рейнольдса меньше 2000, коэффициент трения можно определить по уравнению:
где:
ф — коэффициент трения;
Re — число Рейнольдса;
Когда поток турбулентный и число Рейнольдса выше 4000, коэффициент трения зависит от относительной шероховатости трубы.
а также по числу Рейнольдса.Относительная шероховатость трубы – это шероховатость стенки трубы по сравнению с диаметром трубы e/D .
Так как внутренняя шероховатость трубы фактически не зависит от диаметра трубы, трубы с меньшим диаметром трубы будут иметь более высокую шероховатость.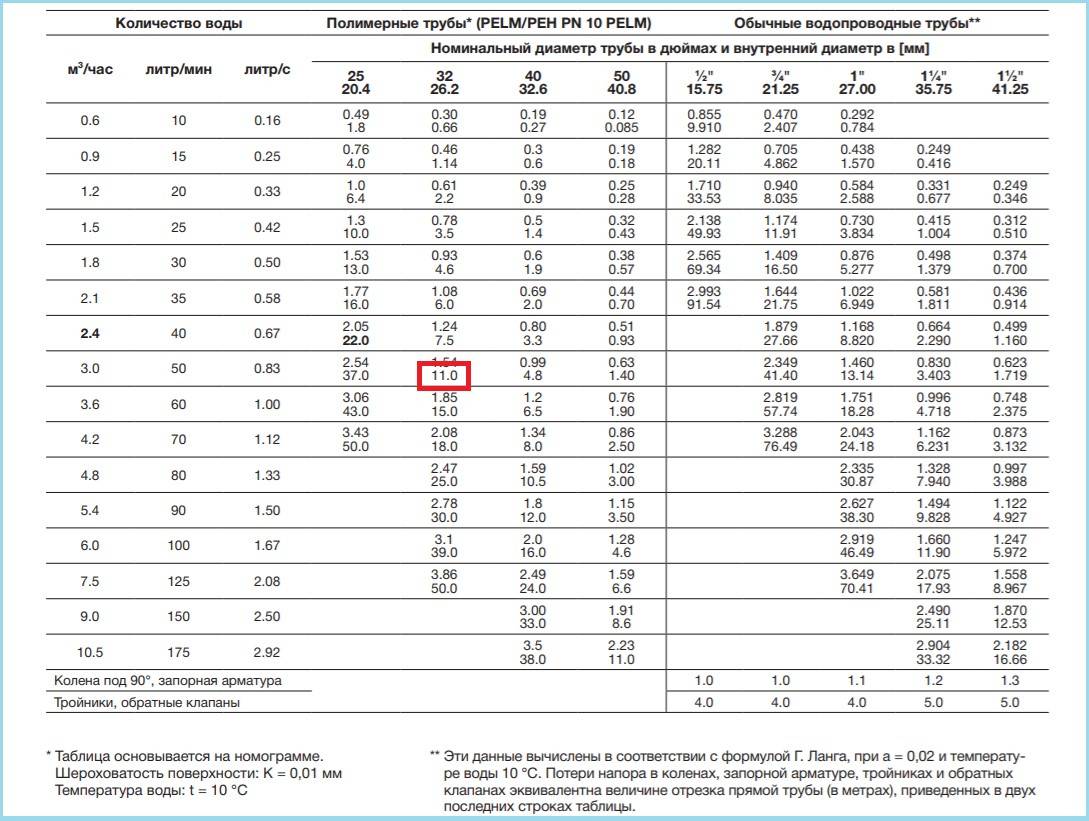
относительная шероховатость, чем у труб большего диаметра, поэтому трубы меньшего диаметра будут иметь более высокий коэффициент трения
чем трубы большего диаметра из того же материала.
Наиболее широко принятыми и используемыми данными для коэффициента трения в формуле Дарси является диаграмма Муди.На диаграмме Муди коэффициент трения
можно определить на основе значения числа Рейнольдса и относительной шероховатости.
Падение давления является функцией внутреннего диаметра в пятой степени. Со временем эксплуатации внутренняя часть трубы
покрывается грязью, окалиной, и часто целесообразно учитывать ожидаемые изменения диаметра.
Также можно ожидать увеличения шероховатости по мере эксплуатации из-за коррозии или образования накипи со скоростью, определяемой материалом трубы.
и характер жидкости.
Когда толщина ламинарного подслоя (ламинарный пограничный слой δ ) больше, чем шероховатость трубы e ,
поток называется потоком в гидравлически гладкой трубе, и можно использовать уравнение Блазиуса:
где:
ф — коэффициент трения;
Re — число Рейнольдса;
Толщина пограничного слоя может быть рассчитана на основе уравнения Прандтля как:
где:
δ — толщина пограничного слоя;
D — внутренний диаметр трубы;
Re — число Рейнольдса;
Для турбулентного течения с Re < 100 000 (уравнение Прандтля) можно использовать:
Для турбулентного течения с Re > 100 000 (уравнение Кармана) можно использовать:
Наиболее распространенным уравнением, используемым для расчета коэффициента трения, является формула Коулбрука-Уайта и
он используется для турбулентного потока в калькуляторе падения давления:
где:
ф — коэффициент трения;
Re — число Рейнольдса;
D — внутренний диаметр трубы;
к р — шероховатость трубы;
Статическое, динамическое и полное давление, скорость потока и число Маха
Статическое давление – это давление жидкости в потоке.
Полное давление — это давление жидкости, когда она находится в состоянии покоя,
то есть скорость уменьшается до 0.
Полное давление можно рассчитать по теореме Бернулли. Представьте себе, что поток находится в одной точке линии тока, остановленной
без потери энергии теорему Бернулли можно записать в виде:
Если скорость в точке 2 v 2 =0, то давление в точке 2 равно сумме p 2 =p t :
где:
р — давление;
р т — общее давление;
v — скорость;
ρ — плотность;
Разница между полным и статическим давлением представляет собой кинетическую энергию жидкости и называется динамическим давлением.
Динамическое давление для жидкостей и несжимаемого потока, где плотность постоянна, можно рассчитать как:
где:
р — давление;
р т — общее давление;
р д — динамическое давление;
v — скорость;
ρ — плотность;
Если динамическое давление измеряется с помощью таких инструментов, как зонд Прандтля или трубка Пито, скорость можно рассчитать в
одна точка линии тока как:
где:
р — давление;
р т — общее давление;
р д — динамическое давление;
v — скорость;
ρ — плотность;
Для газов и чисел Маха больше 0.
1 эффектами сжимаемости нельзя пренебречь.
Для расчета сжимаемого потока можно использовать уравнение состояния газа. Для идеальных газов скорость при числе Маха M < 1 рассчитывается по следующему уравнению:
где:
M — число Маха M=v/c — связь между локальной скоростью жидкости и локальной скоростью звука;
γ — изоэнтропический коэффициент;
Следует сказать, что при М > 0.7 данное уравнение не совсем точно.
Если число Маха М > 1, то возникнет нормальная ударная волна. Уравнение для скорости перед волной приведено ниже:
где:
р — давление;
р ти — общее давление;
v — скорость;
М — Число Маха;
γ — изоэнтропический коэффициент;
Приведенные выше уравнения используются для
Датчик Прандтля и калькулятор скорости потока с трубкой Пито.
Примечание: Вы можете скачать полный вывод данных уравнений
Расход теплоносителя на теплопередачу, мощность котла и температура
Калькулятор тепловой энергии
Рассчитать тепловую энергию и тепловую мощность при известном расходе.Рассчитайте расход для известной тепловой энергии или тепловой мощности.
Применяется для котлов, теплообменников, радиаторов, чиллеров, воздухонагревателей.
Расход жидкости, необходимый для передачи тепловой энергии — тепловой мощности, можно рассчитать как:
где:
q — расход [м 3 /ч];
ρ — плотность жидкости [кг/м 3 ];
c — удельная теплоемкость жидкости [кДж/кгК];
Δ T — разница температур [K];
P — мощность [кВт];
Это соотношение можно использовать для расчета необходимого расхода, например, воды, нагретой в котле, если мощность
котел известен.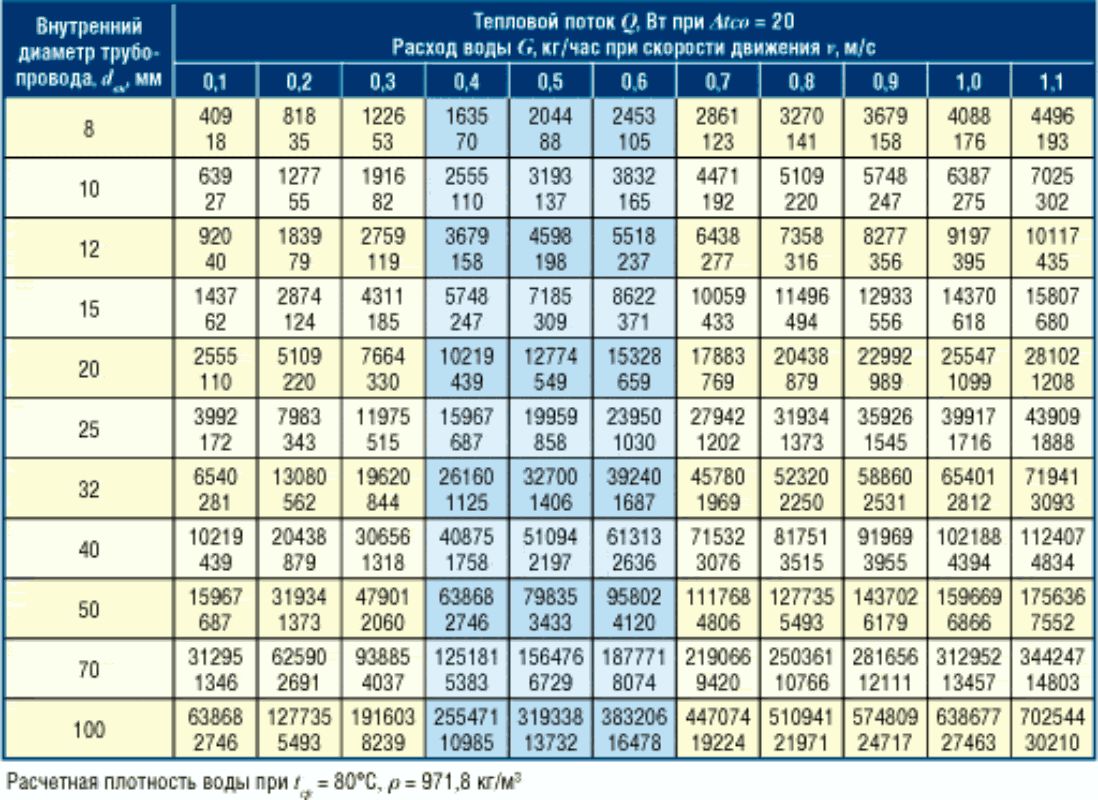
В этом случае разность температур в приведенном выше уравнении представляет собой изменение температуры жидкости впереди и
после котла. Следует сказать, что коэффициент эффективности должен быть включен в приведенное выше уравнение для точного расчета.
Как найти общий объем воды в трубе — OpenFlows | Wiki по водной инфраструктуре — OpenFlows | Водная инфраструктура
| Продукт(ы): | Bentley WaterGEMS, WaterCAD, HAMMER, StormCAD, SewerCAD, SewerGEMS |
| Версия(и): | V8i, версия для подключения |
| Район: | Вывод и отчетность |
Как узнать общий объем воды в моей сети?
WaterCAD, WaterGEMS и HAMMER
Чтобы увидеть общий объем трубы в WaterCAD, WaterGEMS или HAMMER, щелкните меню «Отчет» и выберите Инвентаризация напорных труб .
Это покажет вам общий физический объем всех труб в модели с разбивкой по диаметру и материалу. Поскольку предполагается, что трубы находятся под давлением, это также представляет собой общий объем воды, хранящийся в вашей сети.
Примечание:
1) Объем резервуара необходимо учитывать отдельно. См. поля «Объем полный (расчетный)» или «Объем (расчетный)» в ваших баках.
2) Если вам нужно увидеть общий объем воды, прошедшей через определенный элемент, вам следует вместо этого использовать Суммарный расходомер, доступ к которому можно получить, щелкнув элемент правой кнопкой мыши, или из меню «Анализ».
3) Если вам нужно увидеть общий объем воды, требуемый во время моделирования, см. соответствующее вики-решение ниже:
http://communities.bentley.com/products/hydraulics___hydrology/w/hydraulics_and_hydrology__wiki/finding-total-demanded-volume-for-a-scenario.aspx
StormCAD, SewerCAD, SewerGEMS и CivilStorm
В наших продуктах для ливневых и канализационных систем, чтобы найти общий объем всех труб (некоторые могут называть это пропускной способностью), вам сначала нужно найти общий объем каждой трубы.
2. Для коробки это будет Rise * Span. Если у вас есть микс, вы можете использовать функцию «iif».
После этого вы можете суммировать объем всех каналов, либо скопировав/вставив столбец из гибкой таблицы в электронную таблицу Excel, либо добавив только что созданное поле UDX в гибкую таблицу, затем щелкнув правой кнопкой мыши заголовок столбца и выбрав статистику. Инструкции в приведенной ниже статье описывают, как создать формулу UDX:
.
Создание расширений пользовательских данных на основе формул
Примечание:
1) Вам нужно будет отдельно учитывать объем колодцев, прудов, люков и т. д.См. «Объем полный (вход)» для мокрого колодца. Объем люка также можно рассчитать с помощью расширения пользовательских данных, основываясь на разнице между обратным и ободком и диаметре.
2) Для напорных труб объем можно найти в разделе «Отчет» > «Инвентаризация кабелепроводов и напорных труб» > «Инвентаризация напорных труб».
3) Если вам нужно увидеть общий объем воды, прошедший через конкретный элемент, вы можете использовать средство просмотра гидравлических систем, расположенное в меню «Инструменты».
Труба с переменным объемом жидкости в изотермической жидкостной системе
Описание
Блок частично заполненной трубы (IL) моделирует трубу с возможностью изменения
внутренние уровни жидкости. Труба также может полностью высохнуть во время
моделирование.
В дополнение к жидкостным соединениям в портах A и
B , порт AL принимает уровень жидкости на входе
от соединенных блоков как физический сигнал. Если значение AL равно
больше нуля, A погружен в воду.Если значение при
AL меньше или равен нулю, порт открыт. Труба
уровень жидкости передается как физический сигнал на соединительные блоки в порту
л .
Порт A всегда выше порта B . Если порт
A открывается, трубу можно заполнить через отверстие
Б . Когда жидкость поступает в трубу через порт
B , массовый расход через порт A равен 0
пока труба не будет полностью заполнена, после чего m˙A=m˙B.
Когда использовать блок частично заполненной трубы (IL)
Этот блок можно использовать вместе с блоком Tank (IL) при уровне жидкости
ожидается, что они упадут ниже входного отверстия резервуара. Несколько частично заполненных труб (IL)
блоки также могут быть соединены последовательно или параллельно. Однако, поскольку частично
заполненная труба может быть заполнена только через порт B , если порт
Выявляется одного блока в параллельной конфигурации,
может оказаться невозможным повторно заполнить эту трубу, если ее соединение в порту
B нельзя наполнить трубу.2ρDh3A2.
f — коэффициент трения Дарси для турбулентных течений, который
определяется эмпирической корреляцией Хааланда:
f={−1,8log10[6,9Re+(ε3,7Dh)1,11]}−2,
, где ε — внутренняя поверхность
абсолютная шероховатость . Число Рейнольдса основано на массовом расходе
ставка на порт B и гидравлический диаметр трубы.
Перепад гидростатического давления Δpelev=ρgl.
Массовый расход
Расход в трубе определяется внутренним уровнем жидкости и условиями на
порт B .Труба может быть заполнена или опорожнена в
B , если труба частично пуста. Если труба полностью
заполнен, m˙A=m˙B., и масса сохраняется:
Масса жидкости в трубе определяется относительным наполнением
уровень трубы:
Допущения и ограничения
Этот блок не учитывает динамическую сжимаемость или инерцию жидкости и не учитывает
не моделировать динамику воздуха (или второй жидкости) в трубе.
Расчет объема | SkillsYouNeed
На этой странице объясняется, как рассчитать объем твердых объектов, т.е.е. сколько бы вы могли вместить в предмет, если бы, например, наполнили его жидкостью.
Площадь — это мера того, сколько места находится внутри двухмерного объекта (дополнительную информацию см. на нашей странице: Расчет площади).
Объем — это мера того, сколько места находится внутри трехмерного объекта. Наша страница о трехмерных фигурах объясняет основы таких фигур.
В реальном мире вычисление объема, вероятно, не будет использоваться так часто, как вычисление площади.
Тем не менее, это может быть важно. Возможность рассчитать объем позволит вам, например, определить, сколько места у вас есть для упаковки при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете поместить в банку.
Это также может быть полезно для понимания того, что имеют в виду СМИ, когда говорят о мощности плотины или расходе реки.
A Примечание по модулям
Площадь выражается в квадратных единицах ( 2 ), потому что она измеряется в двух измерениях (т.грамм. длина × ширина).
Объем выражается в кубических единицах ( 3 ), поскольку он измеряется в трех измерениях (например, длина × ширина × глубина). Кубические единицы включают см3, м3 и кубические футы.
Кубические единицы включают 3 см, 3 м и кубические футы.
ВНИМАНИЕ!
Объем также может быть выражен как вместимость по жидкости.
Метрическая система
В метрической системе вместимость жидкости измеряется в литрах, что прямо сравнимо с кубическим измерением, поскольку 1 мл = 1 см 3 .1 литр = 1000 мл = 1000 см 3 .
Имперская/английская система
В имперской/английской системе эквивалентными единицами измерения являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше всего придерживаться либо жидких, либо твердых единиц объема.
Для получения дополнительной информации см. нашу страницу о системах измерения.
Основные формулы для расчета объема
Объем тел на основе прямоугольников
В то время как основная формула площади прямоугольной формы равна длине × ширине, основная формула объема — длине × ширине × высоте.
То, как вы ссылаетесь на различные измерения, не влияет на вычисление: вы можете, например, использовать «глубину» вместо «высоты». Важно то, что три измерения умножаются вместе. Вы можете умножать в любом порядке, который вам нравится, так как это не изменит ответ (дополнительную информацию см. на нашей странице о умножении на ).
Коробка с размерами 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем:
15 × 25 × 5 = 1875 см 3
Объем призм и цилиндров
Эта базовая формула может быть распространена на объем цилиндров и призм .Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.
По сути, для цилиндров и призм объем равен площади одной стороны, умноженной на глубину или высоту формы.
Таким образом, основная формула объема призм и цилиндров:
Площадь торцевой формы × высота/глубина призмы/цилиндра.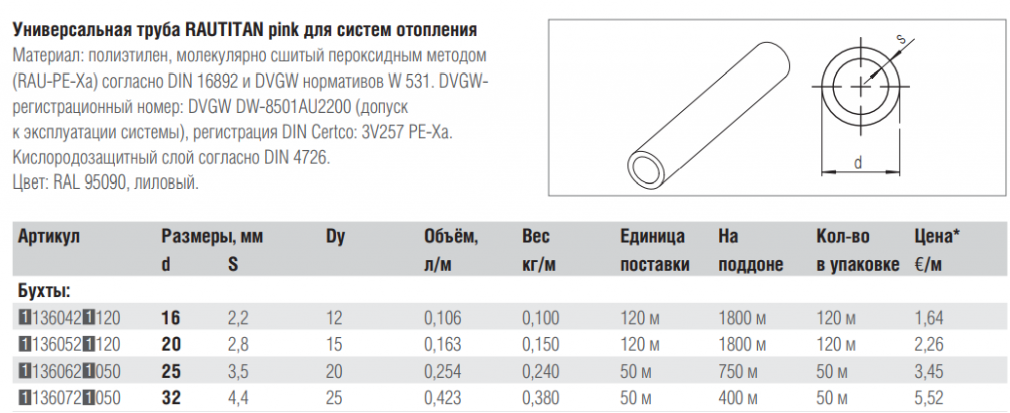
Остерегайтесь несовместимых юнитов!
Прямой отрезок круглой трубы имеет внутренний диаметр 2 см и длину 1 см.7м. Рассчитайте объем воды в трубе.
В этом примере вам нужно рассчитать объем очень длинного тонкого цилиндра, образующего внутреннюю часть трубы. Площадь одного конца можно рассчитать по формуле площади круга πr 2 . Диаметр 2см, значит радиус 1см. Таким образом, площадь равна π × 1 2 , что составляет 3,14 см 2 .
Длина трубы 1,7 м, поэтому вам нужно умножить площадь конца на длину, чтобы найти объем.
Остерегайтесь несовместимых юнитов! Площадь в сантиметрах, а длина в метрах. Сначала преобразуйте длину в см 1,7 × 1000 = 1700 см.
Таким образом, объем равен 3,14 × 1700 = 5338 см 3 . Это эквивалентно 5,338 литра или 0,0053 м 3 .
Объем конусов и пирамид
Тот же принцип, что и выше (ширина × длина × высота), применяется для расчета объема конуса или пирамиды, за исключением того, что, поскольку они сходятся в точке, объем составляет лишь долю от общего объема, который был бы, если бы они продолжали одинаковой формы (в поперечном сечении) насквозь.
Объем конуса или пирамиды составляет ровно одну треть объема коробки или цилиндра с таким же основанием.
Таким образом, формула:
Площадь основания или торца × высота конуса/пирамиды × 1 / 3
Вернитесь к нашей странице Вычисление площади , если вы не можете вспомнить, как вычислить площадь круга или треугольника.
Например, чтобы вычислить объем конуса с радиусом 5 см и высотой 10 см:
Площадь внутри круга = πr 2 (где π (пи) приблизительно равно 3.14, а r — радиус окружности).
В этом примере площадь основания (круга) = πr 2 = 3,14
× 5 × 5 = 78,5 см 2 .78,5 × 10 = 785
785 × 1/3 = 261,6667 см 3
Объем сферы
Как и в случае с кругом, вам нужно π (пи), чтобы вычислить объем сферы.
Формула 4/3 × π × радиус 3 .
Вам может быть интересно, как можно вычислить радиус шара.Если не считать протыкания вязальной спицы (эффективно, но смертельно для мяча!), есть более простой способ.
Вы можете измерить расстояние вокруг самой широкой точки сферы напрямую, например, с помощью рулетки. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.
Длина окружности рассчитывается как 2 x π x радиус.
Чтобы вычислить радиус по длине окружности:
Разделите длину окружности на (2 x π) .
Примеры работы: расчет объема
Пример 1
Вычислите объем цилиндра длиной 20 см с радиусом круглого конца 2,5 см.
Сначала определите площадь одного из круглых концов цилиндра.
Площадь круга равна πr 2 (π × радиус × радиус). π (пи) примерно равно 3,14.
Следовательно, площадь конца:
3.
14 х 2,5 х 2,5 = 19,63 см 2
Объем — это площадь конца, умноженная на длину, и поэтому:
19,63 см 2 x 20 см = 392,70 см 3
Пример 2
Что больше по объему: сфера радиусом 2 см или пирамида с основанием 2,5 см и высотой 10 см?
Сначала определите объем сферы .
Объем сферы равен 4/3 × π × радиусу 3 .
Таким образом, объем сферы равен:
4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51 см 3
Тогда вычислите объем пирамиды .
Объем пирамиды равен 1/3 × площадь основания × высота.
Площадь основания = длина × ширина = 2,5 см × 2,5 см = 6,25 см 2
Таким образом, объем
равен 1/3 x 6,25 x 10 = 20.83см 3
Таким образом, сфера больше по объему, чем пирамида.
Вычисление объема неправильных тел
Точно так же, как вы можете рассчитать площадь неправильных двумерных фигур, разбив их на правильные, вы можете сделать то же самое для вычисления объема неправильных тел. Просто разделите тело на более мелкие части, пока не получите только многогранники, с которыми вам будет легко работать.
Рабочий пример
Рассчитайте объем водяного цилиндра общей высотой 1 м и диаметром 40 см, верхняя часть которого имеет форму полусферы (половина сферы).
Сначала вы делите фигуру на две части: цилиндр и полусферу.
Объем сферы равен 4/3 × π × радиусу 3 . В этом примере радиус равен 20 см (половина диаметра). Поскольку вершина полусферическая, ее объем будет вдвое меньше полной сферы. Таким образом, объем этой секции формы:
0,5 × 4/3 × π × 20 3 = 16 755,16 см 3
Объем цилиндра равен площади основания × высоте.
Здесь высота цилиндра — это общая высота за вычетом радиуса сферы, который равен 1 м — 20 см = 80 см. Площадь основания πr 2 .
Таким образом, объем цилиндрического сечения этой формы:
80 × π × 20 × 20 = 100 530,96 см 3
Таким образом, общий объем этого контейнера для воды составляет:
100 530,96 + 16 755,16 = 117 286,12 см 3 .
Это довольно большое число, поэтому вы можете преобразовать его в 117.19 литров путем деления на 1000 (поскольку в литре 1000см 3 ). Однако вполне корректно выразить ее как cm 3 , так как задача не требует, чтобы ответ был выражен в какой-либо конкретной форме.
Дальнейшее чтение из навыков, которые вам нужны
Понимание геометрии
Часть руководства по необходимым навыкам счета
В этой электронной книге рассматриваются основы геометрии и рассматриваются свойства фигур, линий и тел.
Want to say something? Post a comment
Want to say something? Post a comment